Sбок = пRL, Sосн = пR^2, пRL=3пR^2, L = 3R, L=√R²+h², √R²+h²= 3R, R²+h²=9R²
h = 2R √2,
Vш = 4п(r^3)/3 = 4π*2/3 = 8π/3, Vш = Vк
Vк = πR²h/3 = 8π/3,
R²h = 8, h = 8/R²
R²h = 8
h = 2R √2
R= h/2√2
(h/2√2)²h = 8
h^3/8 =8
h^3 = 64
h = 4
1) 60/13
2) АD=13
3) 60√3
4) 120/13
Объяснение:
ABCD-ромб⇒АС⊥ВD, АО=0,5АС, DО=0,5ВD
АО=0,5АС=0,5·10=5
DО=0,5ВD=0,5·24=12
АС⊥ВD, по теореме Пифагора АD²=АО²+DО²=5²+12²=25+144=169⇒АD=13
2) АВ=ВС=СD=АD=13-сторона ромба
3) Площадь орт.проекции фигуры на плоскость равна произведению площади данной фигуры на косинус угла между плоскостью и данной фигурой.
Площадь ромба по готовой формуле: S=0,5AC·BD=0,5·10·24=120
Площадь орт проекции: s=S·cos((ABCD)∧α)=120·cos30°=120·√3/2=60√3
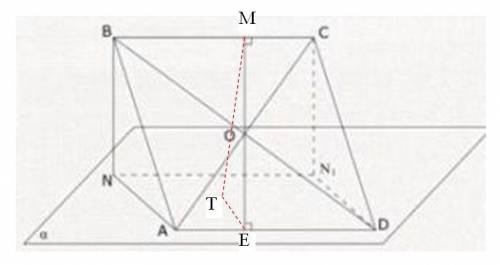
4) Через точку О - пересечение диагоналей ромба проведём перпендикуляр к стороне ВС, OM⊥BC.
Но так как ВС║AD⇒ME⊥AD, ME⊥BC⇒ME-высота ромба.
Ещё одна формула для нахождения площади ромба
S=ME·AD⇒120=ME·AD=13ME⇒ME=120/13
1) Опустим из точки М перпедикуляр МТ на плоскость α.
МТ⊥α, Е∈α⇒отрезок TE есть орт.проекция отрезка МЕ на плоскости α.
АD⊥МЕ⇒АD⊥ТЕ(теорема о трёх перпендикулярах)
Значить, ∠МЕT=(АВСD∧α)=30°
МТ⊥α, ЕТ∈α⇒МТ⊥ ЕТ⇒∠МТЕ=90°
∠МТЕ=90°,∠МЕT=30°⇒MT=0,5ME=0,5 ·120/13=60/13
Растояние между ВD и пл.α и есть отрезок МТ=60/13
Р.S. Все 4 пункта вычислены. Соответствие это выбор подходящего варианта ответа
1-В
2-А
3-Б
4-Д
15см
Объяснение:
Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що з'єднує дану точку з точкою площини і лежить на прямій, перпендикулярній площині. Кінець цього відрізка, що лежить в площині, називається основою перпендикуляраАО-перпендикуляр. АО=12см
Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, що з'єднує дану точку з точкою площини, який не є перпендикуляром до площини.АК -похіла. АК-?
Відрізок, що з'єднує основи перпендикуляра і похилої, проведених з однієї і тієї ж точки, називається проекцією похилої.ОК- проекція похилой. ОК=9 см
АК знайдемо з прямокутного трикутника АКО за теоремою Пифагора:
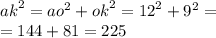
АК=15см
Если считать основание, как ортогональную проекцию боковой поверхности, то угол наклона Ф образующей к основанию сразу вычисляется
Sosn = Sboc*cos(Ф);
cos(Ф) = 1/3;
Отсюда сразу же ctg(Ф) = 1/√8;
радиус основания связан с высотой конуса так r = h*ctg(Ф);
r = h/√8 (ну, или h/(2√2), если очень хочется :).
Объем конуса (1/3)*(π*r^2)*h = (π/3)*h^3/8;
Объем шара радиуса R = 2^(1/3) равен (4π/3)*R^3 = (8π/3);
h^3/8 = 8; h^3 = 64; h = 4;