Вписать в окружность можно только равнобедренную трапецию.
Диагонали равнобедренной трапеции равны, при пересечении образуют с её основаниями равнобедренные треугольники.
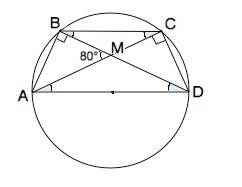
В трапеции АВСD ∆ АМD равнобедренный, его внешний угол при вершине М=80° и равен сумме двух не смежных с ним (свойство внешнего угла).
Углы при основании равнобедренного треугольника равны. =>
угол МАD=углу MDA=80°:2=40°
АD- диаметр, поэтому по свойству вписанного угла ∠АСD=90°
∠АСВ=∠DВC=40° – как накрестлежащие равным углам при АD.
∠АВС=∠ВСD=90°+40°=130°
Cумма углов, прилежащих к боковой стороне трапеции, равна180° =>
угол АDC=180°-130°=50°
ответ: ∠А=∠D=50°, ∠В=∠С=130°.
∠ACB = 65°
Объяснение:
Дано:
В ΔABC (см. рисунок)
∠ABC=∠ABL=61°
∠ALC=88°
Найти: ∠ACB
Решение.
Так как ∠ALC=88°, то смежный с ним угол ∠ALB=180° - 88° = 92°.
Используем свойство: сумма внутренних углов треугольника равна 180°: ∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 92° - 61° = 27°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·27° = 54°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°: ∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 54° - 61° = 65°.
ответ: ∠ACB = 65°.