
Объяснение:
Объем прямой призмы равен произведению площади основания на высоту. Решение данной задачи сводится к нахождению площади трапеции (основания) если известны её основания и боковые стороны.
Найдем высоту трапеции:
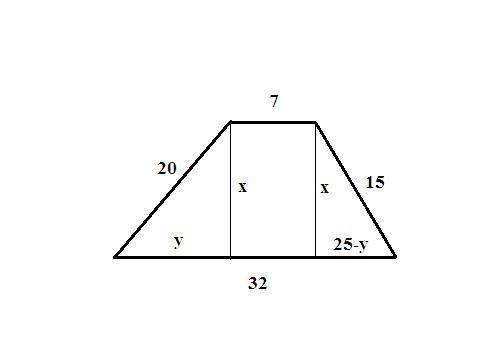
проводим высоты из вершин меньшего основания и обозначим её - х, тогда один отрезок на большем основании - обозначим у, а второй отрезок равен (32-7-у)=(25-у);
треугольники, образованные боковыми сторонами, отрезками большего основания и высотами прямоугольные;
по т. Пифагора:
х²=20²-у²
х²=15²-(25-у)²;
решая данную систему находим у=16, тогда высота - х=12 см;
площадь основания - 12*(7+32)/2=294 см², объем - V=294*2=588 см³.
<CAD=<BCA (как внутренние накрест лежащие при параллельных АВ и CD и секущей АС. Значит и <ВАС=30° (АС - биссектриса) и треугольник АВС равнобедренный. Тогда его высота ВН - это и медиана. Значит ВН - это часть радиуса ВО, так как радиус, перпендикулярный хорде, делит ее пополам. Угол АВС этого треугольника равен 120°. Это вписанный угол, опирающийся на дугу АDC. Значит градусная мера дуги АDC в два раза больше и равна 240°. Тогда градусная мера дуги АВС равна АВС=360°-240°=120°.
На эту дугу опирается центральный угол АОС, соответственно равный 120°. Итак, мы имеем четырехугольник АВСО, являющийся ромбом, и
точка О лежит на стороне АD нашей трапеции. Следоательно
АВ=ВС=АО=ОD=ОС=СD=R=4см. Проведем высоту трапеции СК.
В равностороннем треугольнике ОСD высота СК равна (√3/2)*а, где а=4см. СК=2√3см.
Площадь трапеции S=(BC+AD)*CК/2=12√3см².
ответ: S=12√3см².