Биссектриса острого угла параллелограмма делит его сторону на части длиной 6 см и 2 см, считая от вершины тупого угла. Вычислите площадь параллелограмма, если острый угол 30 градусов.
Биссектриса отсекает от параллелограмма равнобедренный треугольник, следовательно боковая сторона b=6см, а основание а=6+2=8см
Проведем высоту параллелограмма, она лежит в треугольнике против угла 30°
h=b/2=6/2=3. Площадь параллелограмма S=a*h = 8*3 = 24cм²
1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
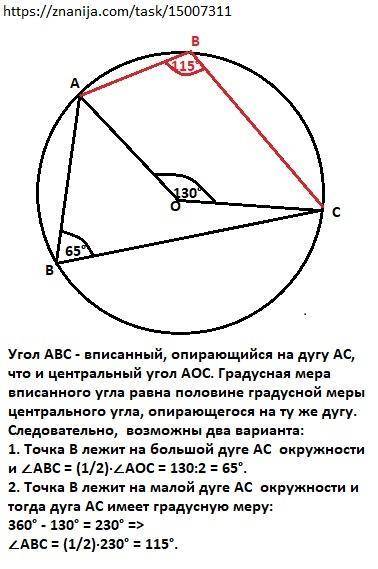
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Использовано свойство накрест лежащих углов при параллельных прямых, признак равнобедренного треугольника, формула площади параллелограмма через синус его угла. Ршение во вложении