
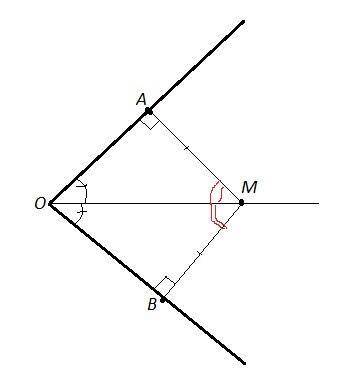
Расстояние от точки М (на биссектрисе) до стороны угла измеряется длиной перпендикуляра, опущенного из этой точки на сторону угла.
∠МАО=∠МВО=90°
∠АОМ=∠ВОМ, так как ОМ- биссектриса.
Соответственно
∠АМО=90°-∠АОМ
∠ВМО=90°-∠ВОМ- как острые углы прямоугольного треугольника
Можем утверждать, что ∠АМО=∠ВМО,
По второму признаку равенства треугольников: сторона и два прилежащие к не угла( ОМ- общая, ∠АМО=∠ВМО и ∠АОМ=∠ВОМ)
ΔАОМ=ΔВОМ. В равных треугольниках против соответственно равных углов лежат равные стороны, отсюда МА=МВ, что и требовалось доказать
Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.

ответ на 2 вопрос
нагаггана