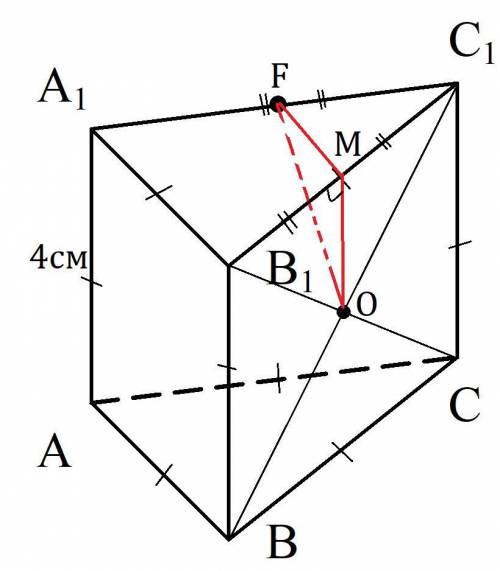
Дано: ABCA₁B₁C₁ - прямая призма с равными рёбрами. F∈A₁C₁; A₁F = FC₁
BC₁∩CB₁ = O
Найти: FO.
Боковые грани призмы это квадраты т.к. рёбра равны и призма прямая.
Пусть M∈B₁C₁ и OM⊥B₁C₁ тогда OM - медиана (т.к. ΔB₁O₁C₁ - равнобедренный), то есть B₁M = MC₁ значит FM - средняя линия ΔA₁C₁B₁.
FM = A₁B₁:2 = 4:2 см = 2см - как средняя линия.
MO = MB₁ - как катет в прямоугольном Δ с острым углом в 45° (ΔB₁OM).
MO = B₁C₁:2 = 4:2 см = 2см.
FM ⊥ MO т.к. призма прямая, то есть линейный угол, двугранного угла между основаниями и боковыми гранями, будет 90°.
По теореме Пифагора в прямоугольном ΔFMO:
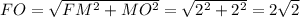 см.
см.
ответ: 2√2 см.
Можно рассуждать по-другому. Есть теорема, по которой произведение площадей треугольников AOB и COD равно произведению площадей треугольников AOD и BOC, откуда неизвестная площадь тр-ка AOD = 6·8/4=12. Доказательство этой теоремы очень простое, основывается на вычислении площади треугольника по формуле "половина произведения сторон и на синус угла между ними", а также на формуле приведения sin (180°-α)=sin α.