Если в трапецию можно вписать окружность, то сумма оснований равна сумме боковых сторон.
Т. к меньшая боковая сторона трапеции равна 10 см, то высота также равна 10 см, абольшая боковая сторона 10: sin45=10: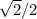 =10
=10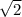
Сумма боковых сторон = сумме оснований и равна 10+10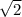 =10(1+
=10(1+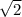
S=(10(1+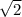 )/2*10=50(1+
)/2*10=50(1+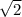 )
)
Т.к. острый угол ромба 60 гр. то диагональ BD отсекает равыносторонний треугольник АВD все его стороны по а Т.к. параллельна ВА , то точка С находится на расстоянииа\2 от С до альфа. Двугранный угол АВ построим его линейный угол. Из D проведём перпендикуляр к АВ это DK Пусть проекция D на альфа будет точка Р Р это основание перпендикуляра. Соединим основание перпендикуляра и основание наклонной получим отрезок КР это проекция на альфа . По теореме о трёх перпендикулярах РК перпендикулярно альфа Тогда угол DKP это линейный угол двугранного угла ВА.sinDKP= DP\DK= а\2: а =1\2 значит угол 30 гр.
Меньшая боковая сторона прямоугольной трапеции 10 см, а острый угол 45 градусов. Найти площадь трапеции, если в нее можно вписать окружность.
Сумма оснований такой трапеции равна сумме боковых сторон.
Высота h = AB = 10 cм, СD = h/sin45 = 10/(√2/2)=10√2 см
BC+AD=AB+CD=10(1+√2) cм
S = (BC+AD)*h/2 = 10(1+√2)*5 = 50(1+√2) cм