Если данный угол FHG, то окружность определяется однозначно. Если угол GFH или HGF , то таких окружностей бесконечно много и радиус не определен. Вернемся к случаю угол FHG=45 градусам. Любой треугольник с углом 45 градусов опирающимся на сторону FG вписан в окружность. Удобно выбрать из них прямоугольный, восстановив перпендикуляр к FG в точке, например,F до пересечения с окружностью в точке Е. Тогда ЕG - диаметр этой окружности, FE=FG=8. Квадрат диаметра равен 64+64=128. Диаметр равен 8*sqrt(2). Радиус равен 4*sqrt(2). Надеюсь, понятно и без рисунка.
Объяснение:
Радиус окружности, описанной около правильного треугольника со стороной а определяется по формуле :
А радиус окружности вписанной в правильный треугольник со стороной а можно найти по формуле :
Значит радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной окружности . Так как по условию
R=8 см, то r =8:2=4 см.
Найдем длину окружности по формуле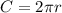 , где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
, где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
Если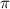 считать приближенно равным 3,14, то
считать приближенно равным 3,14, то
С≈ 8*3,14=25,12 см.