1)
поскольку a||b, то <1=<2
102:2=51°
остальные углы которые вертикальные с углами 1 и 2, также равны 51°
другие 4 угла которые смежные с ними равны 180-51=129°
2)
поскольку <1=<2, можно сделать вывод что m||n
поскольку m||n, то СВ такая же секущая как и АС, значит <3+<4=180
<4=180-120=60°
3)
(на 2 фото рисунок)
поскольку АD биссектриса, то угол DAF=72:2=36°
поскольку АВ||DF, то AD можно считать секущей
углы DAB и АDF внутренне разносторонние, то есть равны
DAB=АDF=36°
F=180-36-36=108°
4)
(на фото рисунок)
для того чтобы параллельные были прямыми, внутренне односторонние углы должны давать в сумме 180°
180-65=115°
угол КЕD=115°

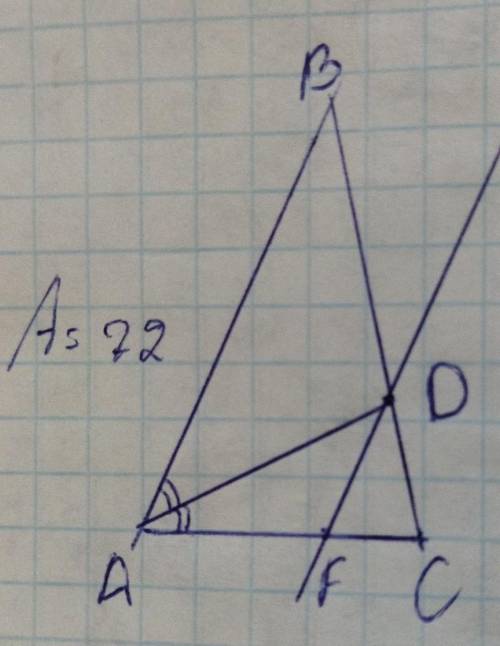
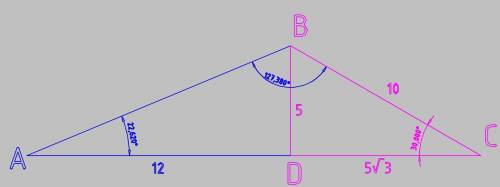
Рассмотрим прямоугольный ΔBCD
CD = 5√3 известный катет
BD - катет против угла в 30 градусов, его длина x
ВС - гипотенуза, её длина 2х
запишем теорему Пифагора для ΔBCD
(5√3)² + x² = (2x)²
25*3 + x² = 4x²
25*3 = 3x²
25 = x²
x = 5
BD = 5
BC = 2x = 10
---
Рассмотрим прямоугольный ΔABD
AD = 12 по условию, катет
BD = 5 из пункта, катет
AB - гипотенуза
по т. Пифагора
AB² = 5² + 12² = 25 + 144 = 169
AB = √169 = 13
---
Периметр ΔABC
P(ΔABC) = AB + BC + CD + AD = 13 + 10 + 5√3 + 12 = 35 + 5√3
---
теорема синусов для ∠A
sin(∠A)/BC = sin(∠C)/AB
sin(∠A)/10 = sin(30°)/13
sin(∠A) = 1/2 /13 * 10 = 5/13
∠A = arcsin(5/13) ≈ 22.6°
---
∠B найдём из того условия, что сумма всех углов треугольника равна 180°
∠B + ∠A + ∠C = 180°
∠B = 180 - ∠A - ∠C = 180 - 22.6 - 30 = 127.4°
Ем-шараменбіргеболады