В прямоугольном треугольнике ABC угол ACB=90° AC=3.найдите разность BC-CD

👇

Увидеть ответ

Ответ:

zolotoy1979

23.11.2021

Объяснение:

С формулы Пифагора:

БС²+АС²=АБ²

АБ=4²+3²=✓25=5

Bc/Ca = Bd/Da

4/3=5-x/x

3(5-x)=4x

15-3x=4x

15=7x

x=15/7

дальше так же по теореме

Если не правильно поправьте меня

4,6(51 оценок)

Открыть все ответы

Ответ:

dinafait2001

23.11.2021

По горизонтали:

1.Перпендикуляр, проведенный из вершина к прямой, на которой лежит противолежащая сторона.

2.Сторона равнобедренного треугольника, не равная двум другим.

3.Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

4.Название науки, произошедшее от греческого слова “землемерие”.

5.Обоснование, логическое рассуждение.

6.Треугольник, у которого 2 стороны равны между собой.

7.Геометрическая фигура, которая состоит из 3-х точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

8.Отрезок, соединяющий центр окружности с ее точкой.

9.Простейшая геометрическая фигура.

По вертикали:

1.Углы, у которых одна сторона общая, а 2 другие являются противоположными лучами.

2.Часть прямой, ограниченная двумя точками.

3.Каждая из частей, на которые делят окружность 2 ее точки.

4.Геометрическая фигура, состоящая из всех точек плоскости, находящихся на расстоянии R от точки О плоскости.

5.Хорда, проходящая через центр окружности.

6.Утверждение, которое обосновывается путем логических рассуждений.

7.Отрезок, соединяющий 2 точки окружности.

8.Луч с началом в вершине угла и делящий этот угол на 2 равных угла.

9.Утверждения, которые принимаются без доказательства.

4,4(3 оценок)

Ответ:

Ivan2367

23.11.2021

(см. объяснение)

Объяснение:

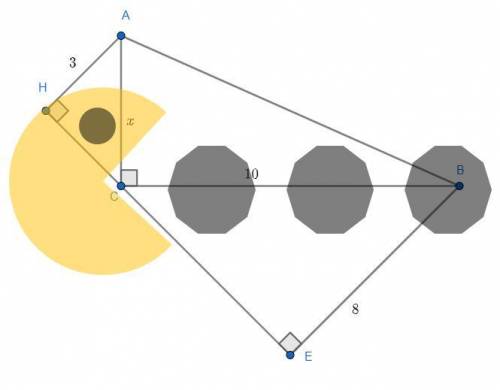
Первый

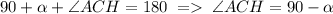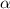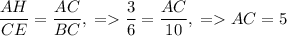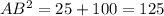Пусть ∠ECB=a. Тогда, т.к. ∠ACB=90°, то $90+\alpha+\angle ACH=180\;=\;\angle ACH=90-\alpha$ . Соответственно $\angle HAC=90-(90-\alpha)=\alpha$ . Значит треугольник AHC подобен треугольнику BEC по двум углам (∠AHC=∠BEC=90° и ∠ECB=∠HAC= $\alpha$ ). Из подобия следует, что $\dfrac{AH}{CE}=\dfrac{AC}{BC},\;=\dfrac{3}{6}=\dfrac{AC}{10},\;=AC=5$ . Тогда по теореме Пифагора для ΔABC: AB^2=25+100=125 .

Приведу решение, в котором используется только теорема Пифагора:

Пусть AC=x. AH=3, а BE=8. Тогда из прямоугольного треугольника AHC 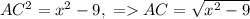$AC^2=x^2-9,\;=AC=\sqrt{x^2-9}$ . Из прямоугольного треугольника BCE 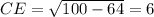$CE=\sqrt{100-64}=6$ . Значит 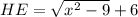$HE=\sqrt{x^2-9}+6$ . Проведем AF - высоту из точки A на BE. Тогда AFEH - прямоугольник => 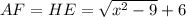$AF=HE=\sqrt{x^2-9}+6$ . По теореме Пифагора для прямоугольного треугольника AFB 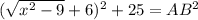$(\sqrt{x^2-9}+6)^2+25=AB^2$ . Но с другой стороны из прямоугольного треугольника ABC 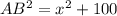AB^2=x^2+100 , т.е. получили уравнение 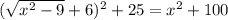$(\sqrt{x^2-9}+6)^2+25=x^2+100$ , откуда x=5, а значит 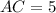AC=5 . 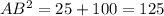Тогда AB^2=25+100=125 .