Объяснение:
По второму признаку равенства треугольников: "Если сторона и два прилежащих к ней угла в одном треугольнике равны стороне и двум прилежащим к ней углам во втором треугольнике - то такие треугольники равны".
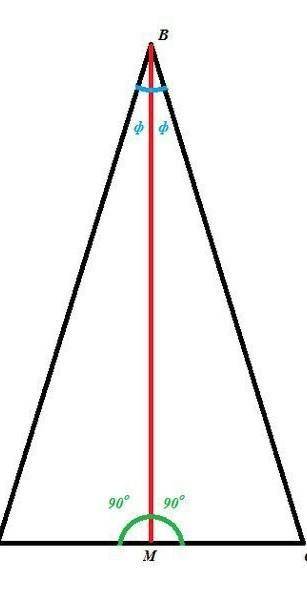
Нам дано, что BM - биссектриса (на рисунке) , значит угол ABM равен углу CBM по определению биссектрисы
Она же есть высота. По определению высоты BM перпендикулярна AC, значит углы AMB и CMB равны между собой (каждый по 90 градусов)
А также сторона BM - общая для треугольников ABM и CBM, значит эти два треугольника равны по 2-му признаку равенства треугольников.
В равных треугольниках против равных углов лежат равные стороны (и наоборот) . Прямые углы AMB и CMB равны, значит и стороны, лежащие против них AB и CB. По определению, треугольник, у которого две стороны равны, называется равнобедренным.
Утверждение доказано.
МОЖНО ЛУЧШИЙ ОТВЕТ!
-------------------
см приложение
α || β ;
B₁B₂ = A₁A₂ + 2 ;
MB₁ = 7 см ;
A₁B₁ =4 см .
--------------
B₁B₂ =x → ?
Так как плоскости α и β параллельны , то будут параллельны и линии пересечении плоскости B₁MB₂ (≡пл A₁MA₂ ) с этими
плоскостями . А отрезки A₁A₂ и B₁B₂ лежать на эти линии , следовательно A₁A₂ || B₁B₂ .
---
ΔA₁MA₂ ~ ΔB₁MB₂ ;
A₁A₂ / B₁B₂ =MA₁ / MB₁ ;
(B₁B₂ -2) / B₁B₂ =( MB₁ -A₁B₁) / MB₁ ;
1 - 2 / B₁B₂ = 1 - 4 /7 ;
2 / B₁B₂ = 4 /7 ;
B₁B₂= 3,5 ( см ) .
ответ : 3,5 см .