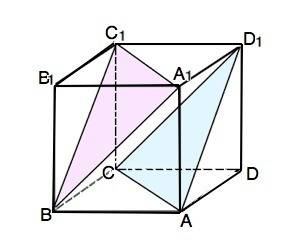
Докажите, что плоскость, проведённая через вершины А, D1 и С куба ABCDA1B1C1D1 параллельна плоскости, проведенной через вершины A1, B и C1
* * *
Диагонали противоположных граней куба, принадлеажщие одной плоскости, параллельны.
АС и А1С1 принадлежат плоскости диагонального сечения куба, А1В||D1C. Параллельны и ВС1 и АD1, принадлежащие плоскости ВС1D1А.
Если две пересекающиеся прямые (АС и АD1) одной плоскости параллельны двум пересекающимся прямым (A1C1 иBC1) (другой плоскости, эти плоскости параллельны.
Если соединить середину основания (любого) с серединой диагонали, то получится отрезок, параллельный боковой стороне (можно указать треугольник, в котором это - средняя линия). В данном случае есть четыре таких отрезка, и они попарно параллельны боковым сторонам, а значит, образуют параллелограмм.
Из условия следует, что в этом параллелограмме диагонали равны, то есть это - прямоугольник.
Далее, ясно, что отрезки, "выходящие" из середины большего основания образуют с ним углы, равные углам при основании трапеции, поскольку каждый из них параллелен одной из боковых сторон.
То есть получилось, что два угла при основании трапеции вместе с углом прямоугольника образуют развернутый угол.
То есть искомая сумма равна 90°