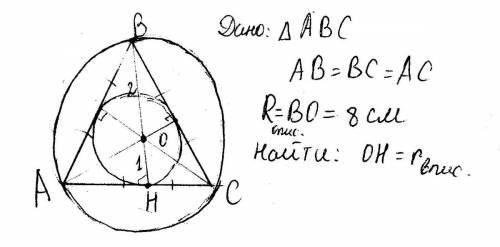
1.Тень от фонарного столба будет 4+8=12м, то есть в 12/4=3 раза больше, чем тень от дерева. Значит и высота столба будет в 3 раза больше дерева, то есть 3*3=9м.
2.Треугольник АВС - прямоугольный.
Докажем это с применением теоремы Пифагора:
41²=40²+9²
1681=1600+81
Значит, АС - гипотенуза.
В прямоугольном треугольнике центр окружности находится посередине гипотенузы, следовательно, радиус окружности равен 41:2=20,5 см.
ответ: 20,5 см
3.(картинка)
4.Опустим из вершины равнобедренного треугольника высоту, которая по известной теореме является медианой и биссектрисой. Тогда из получившихся прямоугольных треугольников найдем, что
sin(α/2) = (x/2)/b = x/(2b), где x - это длина искомого основания. Теперь выразим икс.
x = 2b*sin(α/2).
5.Опускаем перпендикуляр BD на сторону AC.
Проекция AB на AC - это AD= AB cos A; проекция BC на AC - это CD= BC cos C.(Картинка 2)Из теоремы синусов
Объяснение:
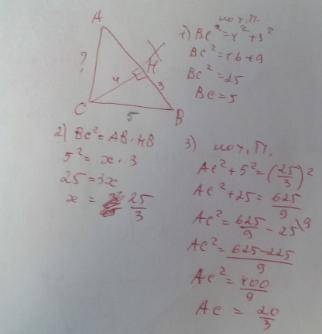
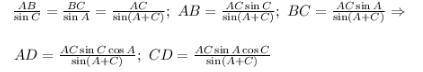
Sabc = 72√3 cм².
Объяснение:
По сумме острых углов прямоугольного треугольника АВС
∠А + 2·∠АВМ = 90°.
Тогда ∠АВМ = 30°, ∠А = 30° и ∠АВС = 60°.
Треугольник АМБ - равнобедренный с основанием АВ и по теореме косинусов
АВ² = АМ²+ВМ² - 2·АМ·ВМ·Cos(∠АМВ).
∠АМВ = 120° => Cos120 = Cos(180-60) = -Cos60.
Cos120 = -(1/2). Тогда АВ² = 192+192+192 = 576.
АВ = √576 = 24см, ВС = (1/2)АВ = 12 см.
Sabc = (1/2)·АВ·ВС·Sin(∠АВС) или
Sabc = (1/2)·24·12·(√3)/2 = 72√3 cм².