
Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
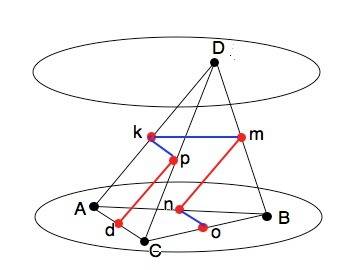
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
32.
Объяснение:
Высоты треугольника пересекаются в одной точке. Продолжим отрезок NO, он пересекает сторону в точке P и также является высотой. Рассмотрим треугольник КМЕ - он прямоугольный, сумма углов треугольника =180 градусам, отсюда находим угол КМЕ =32 градусам. Аналогично рассматриваем треугольник МОР и находим угол МОР = 58.Углы МОР и ЕОN вертикальные, следовательно, равны. Значит угол EON = 58.Рассматриваем треугольник ОEN - он также прямоугольный, и находим угол KNO = 32 градусам.