доклад на тему тригонометрия в музыке
Объяснение:
Тригонометрия в музыке
Доброе время суток! Представляем вашему вниманию интересную информацию о неком методе,который точно обеспечивает связь между тригонометрией и музыкой.
Этот метод анализа музыкальных произведений получил название «геометрическая теория музыки». С его основные музыкальные структуры и преобразования переводятся на язык современной геометрии.
Каждая нота в рамках новой теории представляется как логарифм частоты соответствующего звука (нота «до» первой октавы, к примеру, соответствует числу 60, октава – числу 12). Аккорд, таким образом, представляется как точка с заданными координатами в геометрическом пространстве. Аккорды сгруппированы в различные «семейства», которые соответствуют различным типам геометрических пространств.
При разработке нового метода авторы использовали 5 известных типов музыкальных преобразований, которые ранее не учитывались в теории музыки при классификации звуковых последовательностей – октавная перестановка (O), пермутация (P), транспозиция (T), инверсия (I) и изменение кардинальности (C). Все эти преобразования, как пишут авторы, формируют так называемые OPTIC-симметрии в n-мерном пространстве и хранят музыкальную информацию об аккорде – в какой октаве находятся его ноты, в какой последовательности они воспроизведены, сколько раз повторяются и проч. С симметрий классифицируются подобные, но не идентичные аккорды и их последовательности.
Авторы статьи показывают, что различные комбинации этих 5-ти симметрий формируют множество различных музыкальных структур, одни из которых уже известны в теории музыки (последовательность аккордов, к примеру, будет выражаться в новых терминах как OPC), а другие являются принципиально новыми понятиями, которые, возможно, возьмут на вооружение композиторы будущего.
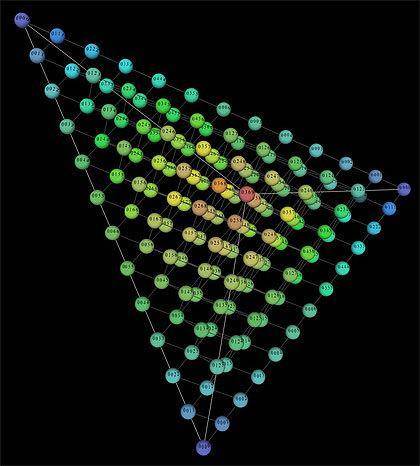
В качестве примера авторами приводится геометрическое представление различных типов аккордов из четырех звуков – тетраэдр. Сферы на графике представляют типы аккордов, цвета сфер соответствуют величине интервалов между звуками аккорда: синий – малые интервалы, более теплые тона – более «разреженные» звуки аккорда. Красная сфера – наиболее гармоничный аккорд с равными интервалами между нотами, который был популярен у композиторов XIX века.
«Геометрический» метод анализа музыки, по мнению авторов исследования, может привести к созданию принципиально новых музыкальных инструментов и новых визуализации музыки, а также внести изменения в современные методики преподавания музыки и изучения различных музыкальных стилей (классики, поп-музыки, рок-музыки и проч.). Новая терминология также более углубленно сравнивать музыкальные произведения композиторов разных эпох и представлять результаты исследований в более удобной математической форме. Иными словами, предлагается выделить из музыкальных произведений их математическую суть.
Этот метод анализа музыкальных произведений получил название «геометрическая теория музыки». С его основные музыкальные структуры и преобразования переводятся на язык современной геометрии.
Каждая нота в рамках новой теории представляется как логарифм частоты соответствующего звука (нота «до» первой октавы, к примеру, соответствует числу 60, октава – числу 12). Аккорд, таким образом, представляется как точка с заданными координатами в геометрическом пространстве. Аккорды сгруппированы в различные «семейства», которые соответствуют различным типам геометрических пространств.
При разработке нового метода авторы использовали 5 известных типов музыкальных преобразований, которые ранее не учитывались в теории музыки при классификации звуковых последовательностей – октавная перестановка (O), пермутация (P), транспозиция (T), инверсия (I) и изменение кардинальности (C). Все эти преобразования, как пишут авторы, формируют так называемые OPTIC-симметрии в n-мерном пространстве и хранят музыкальную информацию об аккорде – в какой октаве находятся его ноты, в какой последовательности они воспроизведены, сколько раз повторяются и проч. С симметрий классифицируются подобные, но не идентичные аккорды и их последовательности.
Объяснение: