
АВСА1В1С1 – прямая треугольная призма, АС = ВС = 10, АВ = 12,
О – точка пересечения медиан, угол C1ОC = 45˚. Найти объем призмы.
-----------
Объем V призмы находят произведением площади её основания на высоту.
V=S•H
В ∆ ОСС1 - угол С1ОС=45º, угол С1СО=90º (т.к. призма прямая и все её ребра перпендикулярны основанию)⇒ второй острый угол ∆ ОСС1 равен 45°. ⇒ ∆ АВС - равнобедренный и СС1=Н=ОС.
Точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины. ⇒
ОС=2/3 медианы СН.
СН в равнобедренном треугольнике - высота, ∆ АНС- прямоугольный.
СН=8 ( отношение катета АН к гипотенузе АС в ∆ АНС= 3:5, следовательно, ∆ АНС - египетский. Можно СН и по т.Пифагора найти)
СС1=ОС=8•2/3=16/3
S (∆ ABC)=CH•AH=8•6=48
V=48•16/3=16•16=256 (ед. площади)

1)Биссектрису, медиану и высоту можно провести в любом треугольнике.
Иногда они могут лежать за пределами треугольника, но провести можно.
2)Если перевернуть равнрбедренный треугольник, то конечно можно провести биссектрису, которая совпадёт с мелианой и высотой. Главное провести из нужной вершины к нужной стороне, чтобы равные стороны были, как бы по бокам.
Объяснение:
Слева стандартный равнобедренный треугольник, где биссектриса, медиана и высота совпадают.
А справа ОН ЖЕ, только на боку. И провести биссектрису, которая совпадёт с медианой и высотой, можно ТОЛЬКО из той же вершины.
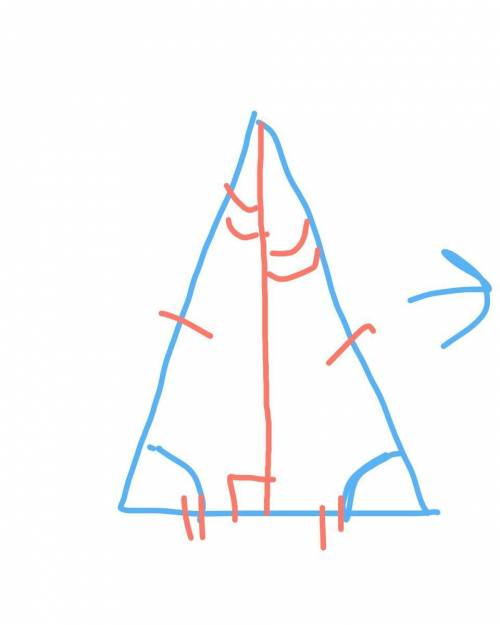
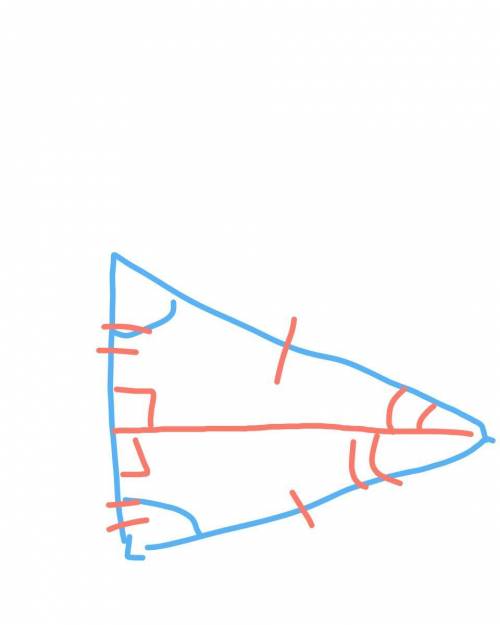
На чертеже.
Объяснение:
Возьмём х - каждый угол,тогда:
5х+2х+5х=180 (Т.к. сумма углов треугольника равна 180)
12х=180
х=15
Подставляем найденный х к 5:2:5, получаем:
1) 5×15=75 - угол А
2) 2×15=30 - угол В
3) 5×15=75 - угол С
Есть свойство: в равнобедренном треугольнике углы при основании равны,углы при основании - А и С,значит треугольник равнобедренный.
Самая длинная сторона - боковая,в данном случае их две АВ и ВС,т.к. они равные. (Также по свойству: против большего угла лежит большая сторона)