Диагонали ромба перпендикулярны (докажите самостоятельно). Диагонали ромба точкой пересечения делятся пополам (это верно для любого параллелограмма - докажите самостоятельно). Пусть одна диагональ ромба d см, тогда вторая диагональ (по условию) (d+8) см. Диагонали ромба делят ромб на четыре равных прямоугольных треугольника. Каждый такой прямоугольный треугольник имеет катеты (d/2) и (d+8)/2 см, и гипотенузой 20 см. По т. Пифагора получим (d/2)^2 +( (d+8)/2)^2 = 20^2; решаем это уравнение (d²/4)+ (1/4)*( d² + 16*d + 64) = 400, d² + d² + 16d + 64 = 4*400 = 1600, 2*d² + 16d + 64 - 1600 = 0, d² + 8d + 32 - 800 = 0, d² + 8d - 768 = 0, D = 8² - 4*(-768) = 64+3072 = 3136 = 56², d₁ = (-8 - 56)/2 = -64/2 = -32, (этот корень не годится, т.к. он отрицательный: длина отрицательной быть не может) d₂ = (-8 + 56)/2 = 48/2 = 24. Итак, d = 24 см это первая диагональ, вторая диагональ (d+8) = 24+8 = 32 см. Площадь найдем по известной формуле: площадь ромба равна половине произведения его диагоналей. S = (24*32)/2 = 12*32 см² = 384 см²
ΔABC; медианы AA_1 и BB_1; пересекаются в точке G. Через A_1 проводим прямую, параллельную BB_1, пересекающую AC в точке D.Угол ACB пересекается параллельными прямыми⇒по теореме о пропорциональных отрезках B_1D:DC=BA_1:A_1C=1:1⇒B_1D=DC⇒AB_1=2B_1D. Угол CAA_1 пересекается параллельными прямыми⇒по теореме о пропорциональных отрезках AG:GA_1=AB_1:B_1D=2:1. Таким образом, медиана BB_1 в точке пересечения разделила медиану AA_1 в отношении 2 к 1, считая от вершины. Поскольку мы взяли две произвольные медианы, доказано, что каждая из них разделит каждую в отношении 2 к 1. Поэтому во-первых они пересекаются в одной точке, а во-вторых, делятся точкой пересечения в отношении 2 к 1, считая от вершины. Замечание для продвинутых (21+)))Знающие теорему Чевы вопрос о том, что медианы пересекаются в одной точке, не задают. А знающие к тому же теорему Менелая, не спрашивают и про отношение 2 к 1. А знающие теорему Ван-Обеля просто умирают при этом со смеху, потому что для них решение прокручивается устно в голове за 0,5 секунды максимум
Формула вычисления длины дуги, зная радиус, и центральный угол: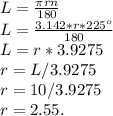
Вывод: Радиус равен — 2.55.