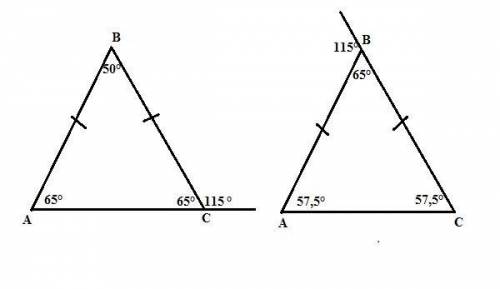
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
Рассмотрим 2 треугольника: АВВ1, АОС1:
- оба прямоугольные
- уголВАО общий
известно, что сумма острых углов прямоугольного треугольника величина постоянная (равна π/2), или:
уголАВВ1+уголВАВ1=уголАОС1+уголС1АО(=π/2),
очевидно: уголВАВ1≡уголС1АО(≡ВАО), уголАВВ1≡уголАВС, уголАОС1≡уголАОС⇒получаем:
уголАВС+уголВАО=уголАОС+уголВАО,
уголАВС=уголАОС, ч.т.д
или вот так:
уголВСС1=уголОСВ1 (вертикальные при пересекающихся ОС1иВВ1))
Тогда π/2-уголВСС1=π/2-уголОСВ1,
а из треугольников(прямоугольных) ΔВСС1, ΔОСВ1 получим, что эти углы равны тем которые нам надо сравнить:
уголАВС=уголАОС, ч.т.д
2) это утверждение верно, только если АС=СВ, то есть нам дан равнобедренный тупоугольный треугольник.