80°, 65°, 35°
Объяснение:
Используем теорему о сумме углов треугольника. Сумма всех углов треугольника равна 180°.
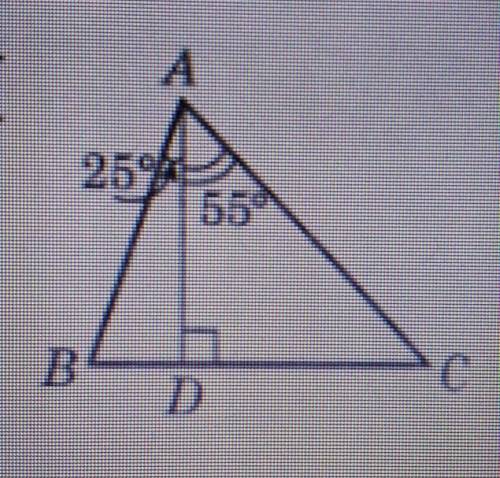
В треугольнике ABD угол BAD = 25°, угол BDA = углу ADC = 90°. Значит, угол ABD = 180° - (90° + 25°) = 65°.
В треугольнике ACD угол CAD = 55°, угол CDA = 90°. Значит, угол ACD = 180° - (90° + 55°) = 35°.
Угол BAC = угол BAD + угол DAC = 55° + 25° = 80°
1) Найдем, через соотношение отрезков, их длины:
32 --- 5, значит, х --- 2 ⇒ х = 12,8 см
32 --- 5, значит, х --- 3 ⇒ х = 19,2 см
2) Мы видим, что эти отрезки являются средними линиями получившихся треугольников. По свойству средней линии в треугольнике она равна половине основания. В данном случае основания треугольников - это основания трапеции. Найдем их:
12,8*2 = 25,6 см
19,2*2 = 38,4 см
Проверка:
Средняя линия трапеции равна полусумме оснований:
С.лин. = 38,4+25,6/2 = 64/2 = 32 см. Все сходится.
ответ: 38,4 см, 25,6 см.
ответ:BCA=90( сумма острых углов прямоугольного треугольника) -55(ADC)=35.
BAD+ADC=55+25=80.=BAC.
ABC=180(сумма углов треугольника) -BAC-ACB=180-35-80=65.
Объяснение: