Контрольна робота з геометрії 8 класу з теми «Подібність трикутників» містить два варіанти по 7 завдань в кожному, 4 з яких – тестові, 3 – вимагають повного розв’язання і обгрунтування
Варіант 1
(3б.) Заповніть пропуски:
а) Якщо ∆ABC ∆MNK, то B = …, M = …, C = …;
б) якщо ∆ABC ∆MNK, то ;
в) Якщо BD — бісектриса кута ABC (рис. 1), то .
У завданнях 2—4 виберіть правильну відповідь. (Кожне завдання оцінюється 1 б.)
∆АВС ∆А1В1С1, АС = 8 см, А1В1 =12 см, В1С1 =14 см, А1С1= 16 см. Знайдіть сторони АВ і ВС.
а) 24 см, 28 см; б) 6 см, 7 см; в) 14 см, 16 см.
∆АВС ∆А1В1С1, АВ = 7 см, ВС = 6 см, АС = 5 см. Знайдіть периметр трикутника A1B1C1, якщо В1С1 = 2 см.
а) 6 см; б) 24 см; в) 36 см.
Катет прямокутного трикутника дорівнює 10 см, а його проекція на гіпотенузу — 8 см. Знайдіть гіпотенузу цього трикутника,
а) 1,25 см; б) 6 см; в) 12,5 см.
Розв’яжіть задачі 5—7 з повним поясненням.
(1 б.) За даними рис. 2 доведіть подібність трикутників ABE і CDE.
(2 б.) Дві сторони трикутника дорівнюють 6 см і 8 см. Бісектриса трикутника, що проведена до третьої сторони, поділяє її на відрізки, більший з яких дорівнює 4 см. Знайдіть периметр трикутника.
(3 б.) В трапеції ABCD її основи AB і CD дорівнюють відповідно 9 см і 12 см, а одна з діагоналей дорівнює 14 см. На які відрізки ділиться ця діагональ точкою перетину діагоналей?
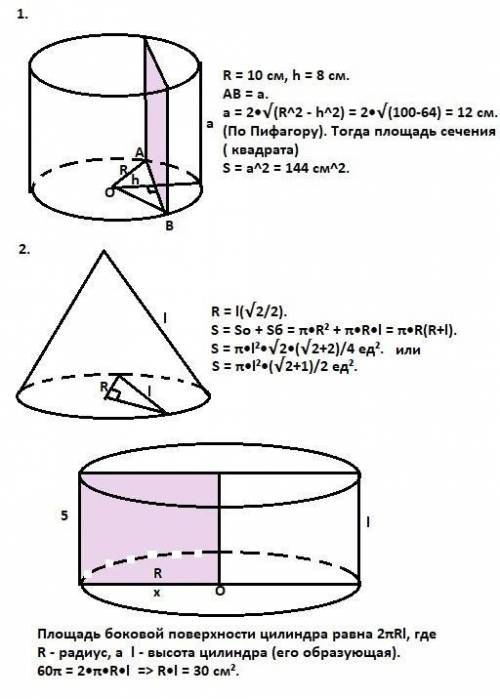
1. S = 144 см².
2. S = π•l²•(√2+1)/2 ед².
3. S = 30 см².
Объяснение:
Радиусы основания цилиндра, проведенные к концам хорды, являющейся стороной квадрата, образуют равнобедренный треугольник с основанием, равным этой стороне. Высота этого треугольника равна расстоянию от центра основания цилиндра до хорды. В равнобедренном треугольнике высота является и медианой. Следовательно, сторона квадрата равнa
а = 2•√(R^2 - h^2) = 2•√(100-64) = 12 см. (По Пифагору). Тогда площадь сечения ( квадрата) равна
S = a^2 = 144 см².
2. Площадь боковой поверхности конуса равна Sбок = π•R•l, а площадь основания конуса равна So = π•R², где R - радиус основания конуса, а l - его образующая. Хорда и проведенные к ее концам радиусы образуют равнобедренный прямоугольный (дано) треугольник с гипотенузой, равной этой хорде. Тогда по Пифагору гипотенуза этого треугольника равна l = R•√2, а катеты (радиусы основания) соответственно равны R = l•√2/2. Тогда площадь полной поверхности конуса равна
S = So + Sб = π•R² + π•R•l = π•R(R+l).
S = π•l²•√2•(√2+2)/4 ед² = π•l²•(√2+1)/2 ед².
3. Площадь боковой поверхности цилиндра, полученного вращением прямоугольника вокруг одной из его сторон, равна S = 2•π•R•l, где R - радиус основания цилиндра, а l - его высота. В нашем случае и радиус и высота - стороны прямоугольника, одна из которых равна 5 см. Тогда (независимо от того, чему равна одна из сторон прямоугольника) имеем:
60π = 2•π•R•l => R•l = 30 см². Это и есть площадь прямоугольника, вторая сторона которого в нашем случае равна 6 см.
Необходимость, обязанность отвечать за свои действия, поступки, быть ответственным за них.
Объяснение: