Если нельзя применить теоремы синусов и косинусов, то, скорее всего, можно применить теорему Пифагора.
Пусть высота треугольника АВС из точки А равна Н.
Опустим из основания биссектрисы перпендикуляр h на сторону ВС.
Из подобия треугольников имеем h/H = 4/20 = 1/5,
По Пифагору находим:
Н = √(20² - (5/2)²) = √(400 - (25/4) = √(375/4) = 15√7/2.
Теперь получаем: h = (1/5)*(15√7/2) = 3√7/2.
Длину биссектрисы L тоже определяем по Пифагору.
Проекция её на ВС равна (5/2) + (4/5)*(5/2) = 9/2.
L = √((9/2)² + h²) = √((81/4) + (63/4)) = √(144/4 = √36 = 6.
ответ: длина биссектрисы равна 6.
Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.
Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик) , от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус» , а термин «линия» возник от латинского «линум» (льняная нить) .
Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами; при изготовлении технических чертежей — выполнять геометрические построения. И если ты, юный читатель, хорошо изучил курс геометрии, то не останешься безоружным, когда при решении практических задач потребуется применить геометрические теоремы или формулы.
Объяснение:
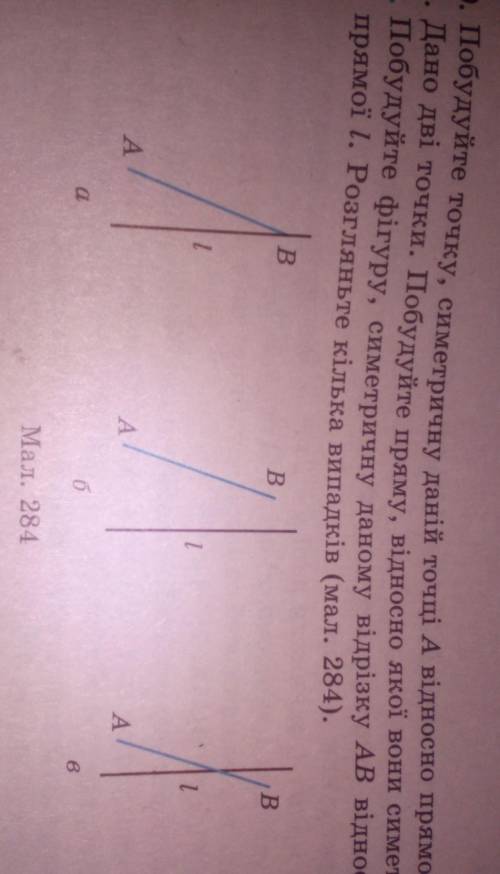
Берём линейку и отмеряем одинаковые отрезки до линии l и после линии.
Красным отмечены одинаковые отрезки
А синяя линия это симметрия.