1) Через две точки можно провести только одну прямую (аксиома).
При расположении точек важно, чтобы ни одни три не располагались на одной прямой.
Как вариант построения:
Наложите два треугольника один на другой так, чтобы они не имели общих вершин и их стороны пересекались. Вершины треугольников можно попарно соединять в разных комбинациях (см. рисунок в приложении)
2) Через любые две точки проходит одна и только одна прямая. (Аксиома).
Пересекающиеся прямые имеют только одну общую точку. В противном случае , если бы они имели две общие точки, то через эти точки проходили бы две различные прямые, что противоречит аксиоме.
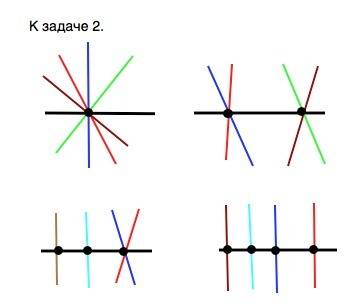
Отсюда следуют варианты:
а) все четыре прямые пересекают данную в одной точке.
б) прямые пересекают её в двух точках ( по две в каждой)
в) в трёх точках ( две из них пересекают прямую в одной точке)
г) в четырех точках -каждая прямая пересекает данную в отдельной точке.
При пересечении четырех прямых с данной может образоваться от одной до четырех точек пересечения.

Окружность разделена точками А,В,С и D на отрезки (дуги) с градусной величиной 60°, 80°, 100° и 120° , то есть дуга АВ = 60°, ВС = 80°, CD = 100° и DA=120°. (так как 3+4+5+6=18, 360°/18=20°, ну и 20*3=60° и так далее...)
Углы, вписанные в окружность, опирающиеся на соответствующие дуги, равны половине их градусной величины.
Значит угол ВСD = (BA+AD)/2 = 180°/2=90°
угол АВС = (AD+DC)/2 = 220°/2=110°. Тогда угол МСВ = 90°(как смежный с 90°) а угол МВС = 70° (как смежный с 110°) (точка М - точка пересечения прямых АВ и CD) Тогда искомый угол ВМС = 180°-90°-70° =20°. (так как в треугольнике сумма углов = 180°)
ответ 20°
Объяснение:
№1
Даны треугольники АВС и А1В1С1 в которых стороны АС и А1С1, высоты ВН и В1Н1 и медианы ВМ и В1М1 равны.
Прямоугольные треугольники НВМ и Н1В1М1 равны по 4-му признаку равенства, так как у них гипотенузы (ВМ и В1М1) и катеты (ВН и В1Н1) равны (дано). => HM=H1M1 и <BMH=<B1M1H1. Значит равны и углы ВМС и В1М1С1 как смежные с равными.
АМ=МС=А1М1=М1С1 как половины равных отрезков АС и А1С1.
Треугольники АВМ и А1В1М1 равны по двум сторонам (АМ=А1М1, ВМ=В1М1) и углу между ними (<BMH=<B1M1H1 - доказано выше) => АВ = А1В1.
Треугольники ВМС и В1М1С1 равны по двум сторонам (МС=М1С1, ВМ=В1М1) и углу между ними (<BMС=<B1M1С1 - доказано выше) => ВС = В1С1.
Тогда треугольники АВС и А1В1С1 равны по трем сторонам, что и требовалось доказать.