6√3
Объяснение:
Проведём высоту к основанию. Она разделит треугольник на два прямоугольных треугольника с катетом 9 и острым углом 60 (половина основания и половина противолежащего угла соответственно). Гипотенуза такого треугольника равна 9/sin60=6√3, а второй катет равен (6√3)*cos60=3√3. Площадь исходного треугольника равна площади 2 его половинок - прямоугольных треугольников, а площадь прямоугольного треугольника равна произведению катетов. Тогда S=1/2*2*9*3√3=27√3, а боковая сторона равна 6√3.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Как это получается?
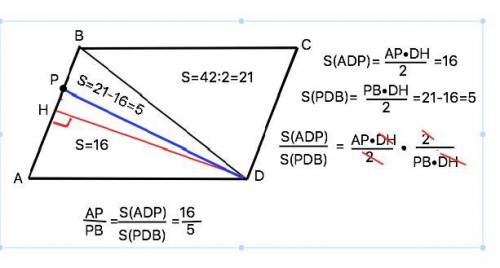
Объяснение: Диагональ ВD делит параллелограмм площадью 42 ед. на два равных треугольника. Площадь каждого 42:2=21 ед.
Ѕ ∆ АРD = 16 ед (дано), => Ѕ ∆ РВD=21-16=5 (ед).
Треугольники АРD и РВD имеют общую высоту DH. Соответственно:
S(ADP)=AP•DH:2
S(PBD)=PB•DH:2 => S(ADP):S(PBD)=(AP•DH:2):(PB•DH:2) = АР:РВ =>
АР:РВ=S(ADP):S(PBD)=16:5 (см. рисунок приложения).
2) They are working
3) My parents are playing golf
4) Charli is recording
5) President is speaking
6) look, your sister is baking
7) it is raining now
8) I am listening
9) Gan is running
10) My dog is playing