Один из катетов прямоугольного треугольника равен 30 см, а радиус описанной вокруг него окружности - 17 см. Вычислить площадь данного треугольника.
Гипотенуза треугольника является диаметром описанной окружности.
Второй катет b = √34²-30²=√256=16 cм
Площадь тр-ка S = a*b/2 = 30*16/2 = 240см²
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение:
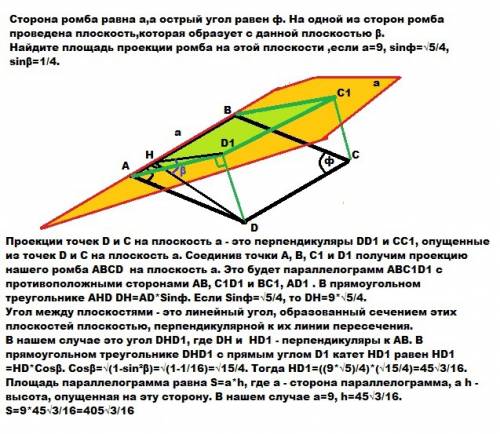
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы. Т.к. R=17 см, то гипотенуза = 34 см. По т. Пифагора второй катет равен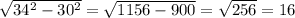 см
см
S=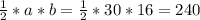 см^2
см^2