У равностороннего треугольника все стороны и углы равны между собой, внешние углы треугольника АВС также равны между собой и равны 120°
Стороны треугольников МКВ, МАР и РСК также равны МВ=СК=АР=3*АВ,
МА=КВ=СР=2*АВ - следовательно ΔМКВ=ΔМАР=ΔРСК.
У равных треугольников соответствующие стороны равны, значит
МР=РК=МК. Что и требовалось доказать.
r=4 см
Объяснение:
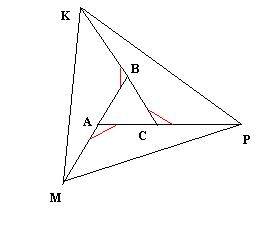
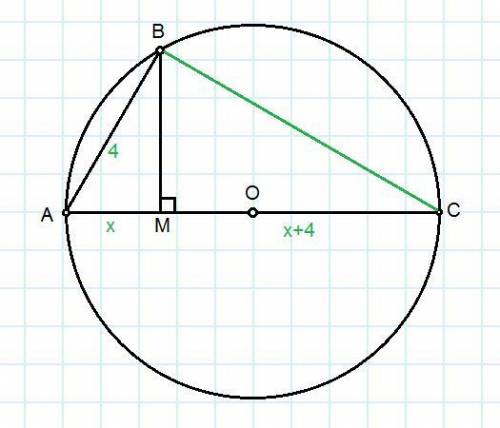
Дано: АС - диаметр окружности, точка В лежит на окружности, ВМ⊥АС, СМ=АМ+4.
Найти: r.
Рисунок к задаче смотри в прикрепленном файле.
Пусть АМ=х, тогда МС=х+4.
ΔАВМ прямоугольный, т.к. ВМ⊥АС (по условию).
По теореме Пифагора найдем ВМ.
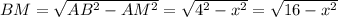
Проведем отрезок ВС. ΔАВС прямоугольный, т.к. вписан в окружность и одна его сторона является диаметром окружности.
ВМ - высота, проведенная из вершины прямого угла к гипотенузе - вычисляется как корень квадратный из произведения длин отрезков, на которые высота поделила гипотенузу.
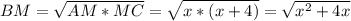
Мы получили два разных выражения, при которых можно найти длину отрезка ВМ. Поскольку результат у них будет одинаковый, приравняем их.
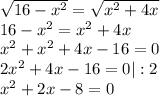
По теореме Виета x₁=-4, х₂=2.
х=-4 - посторонний корень (т.к. длина отрицательной быть не может).
АМ=2, МС=2+4=6.
АС=АМ+МС=2+6=8
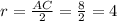
ответ: r=4 см.
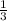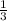(см²). см². 
Я, конечно, понимаю, что требуется "умное" решение, но всё-таки... :)))
При повороте плоскости на 60 градусов вокруг центра треугольника АВС вся фигура (вместе с продолжениями) перейдет в себя (ну, если повернуть по часовой стрелке, то А прейдет в В, М в К, В в С, К в Р, С в А, Р в М... а можно и против часовой повернуть). Поэтому все расстояния МК=МР=КР равны (еще раз - существует такое преобразование без сжатия, при котором эти отрезки совпадают, поэтому они равны). Это полностью исчерпывает доказательство.