60 ед²
Объяснение:
Пусть прямоугольный треугольник АВС. Угол С=90°. Точка касания делит гипотенузу на отрезки: х и 17-х. Отрезки катетов от вершин А и В до точек касания равны х и 17-х, как касательные, проведенные из одной точки. Отрезки катетов от вершины С до точек касания равны радиусу вписанной окружности, то есть равны 3. Тогда катеты равны х+3 и 17-х+3 = 20-х. По Пифагору:
(х+3)² + (20-х)² = 17² => x² - 17х +60 =0. =>
х1=5, х2 =12. => катеты равны 8 и 15 ед. в обоих случаях.
Sabc = (1/2)*8*12 = 60 ед².
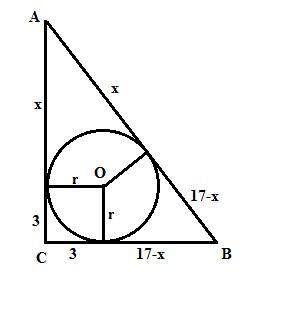
Вообще небольшая ошибка. На рисунке угол 80 градусов, а в условии 90
1. Если угол 80 градусов:
Точки A и B являются касательными к окружности. Радиус, проведенный к точке описанной окружности образует с касающей угол 90 градусов, то есть углы OAC и OBC равны по 90 градусов.
Сумма углов четырёхугольника равна 360 градусов. Мы знаем 3 угла, нам нужно найти 4-ый.
Угол ACB = 360 - 80 - 90 - 90 = 100 градусов
2. Если угол 90 градусов:
Точки A и B являются касательными к окружности. Радиус, проведенный к точке описанной окружности образует с касающей угол 90 градусов, то есть углы OAC и OBC равны по 90 градусов.
Сумма углов четырёхугольника равна 360 градусов. Мы знаем 3 угла, нам нужно найти 4-ый.
Угол ACB = 360 - 90 - 90 - 90 = 90 градусов