Треугольник АВС, АВ=ВС, АС=12, высота=медиане = ВН, АН=СН = 12/2=6
АВ=АС=а,
Периметр = а+а+12=2а+12, полупериметр=(2а+12)/2 = а+6
радиус= площадь/полупериметр
площадь = радиус х полупериметр = 3 х (а+6) = 3а+18
ВН = корень(АВ в квадрате - АН в квадрате) = корень(а в квадрате - 36)
площадь = 1/2АС х ВН = 6 х корень(а в квадрате - 36)
приравниваем площади
3а+18 = 6 х корень(а в квадрате - 36) - возводим две части в квадрат
27а в квадрате - 108а -1620=0
а = (108+- корень(11664+ 4 х 27 х 1620) ) / 2 х 27
а= (108+- 432) / 54
а = 540/54 =10 = АВ=АС
высота ВН = корень(100-36) = 8
площадь = 1/2 х 12 х 8 = 48
Чертеж к решению - во вложении.
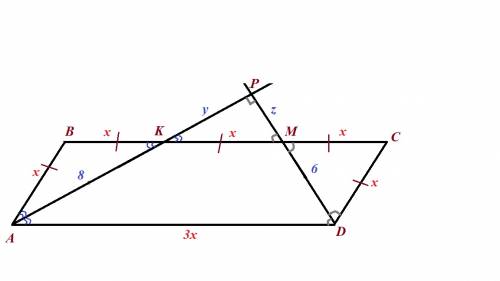
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
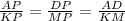
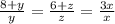
1) 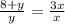
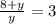
3y=8+y
y=4,
2) 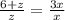
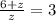
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
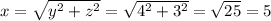
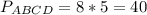
ответ: 
Построим сечение плоскостью через точки PMB
X - пересечение BP и AC
K - пересечение XM и DC
KMB - сечение
PT||BM, QT - искомый отрезок
В плоскости ABC:
проведем NY||BX
CY/YX =CN/NB =1
AY/YX =AN/NP =6/1
CY=YX=x, AY=6x, AC=5x => AC/CX =5/2
проведем NZ||AX
XZ/ZB =CN/NB =1
XZ/ZP =AN/NP =6/1
XZ=ZB=6x, ZP=x, PB=5x => XP/PB =7/5
В плоскости ADC:
AC/CX *XK/KM *MD/DA =1 (т Менелая) => 5/2 *XK/KM *1/2 =1 => XK/KM =4/5
В плоскости сечения KMB:
XT/TM =XP/PB =7/5 => TM/XM =5/12
XK/KM =4/5 => KM/XM =5/9
TM/KM =5/12 *9/5 =3/4 => KT/TM =1/4
QT/BM =KT/KM =1/4 => QT =1/4 a