Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
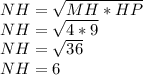
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
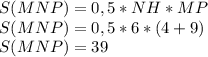
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
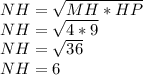
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
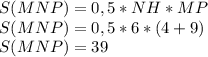
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
ответ:3см
CD-диаметр, OC=OA=OВ=OD-радиусы⇒OC=0,5CD=0,5·6=3 см
∠BOC+∠AOC=180° (смежные углы)
∠AOC=180°-∠BOC=180°-120°=60°
OA=OC(как радиусы)⇒ΔOAC-равнобедренный⇒∠A=∠C
∠A+∠AOC+∠C=180°
∠A+60°+∠A=180°
2∠A=180°-60°=120°
∠A=∠C=60°⇒∠A=∠C=∠AOC=60°⇒ΔAOC-равносторонний⇒
⇒AC=OA=OC=OD=3 см
Объяснение: