а) Xm=(Xa+Xb)/2 = (4-2)/2=1. Ym=(Ya+Yb)/2= (5-1)/2=2. M(1;2). Xk=(Xa+Xb)/2 = (-2-2)/2=-2. Yk=(Ya+Yb)/2= (5+3)/2=4. K(-2;4).
б) |MC|=√[(Xc-Xm)²+(Yc-Ym)²]=√[(-2-1)²+(3-2)²]=√10.
|KB|=√[(Xb-Xk)²+(Yb-Yk)²]=√[(4+2)²+(-1-4)²]=√61.
в) |MK|=(1/2)*|BC|. |BC|=√[(Xc-Xb)²+(Yc-Yb)²]=
√[(-2-4)²+(3+1)²]=√52. |MK|=√52/2=√13.
Или так: |MK|=√[(Xk-Xm)²+(Yk-Ym)²]=√[(-2-1)²+(4-2)²]=√13.
г) |AB|=√[(Xb-Xa)²+(Yb-Ya)²]=√[(4+2)²+(-1-5)²]=6√2. |BC|=√[(Xc-Xb)²+(Yc-Yb)²]=√[(-2-4)²+(3+1)²]=√52.
|AC|=√[(Xc-Xa)²+(Yc-Ya)²]=√[(-2+2)²+(3-5)²]=2.
Объяснение:
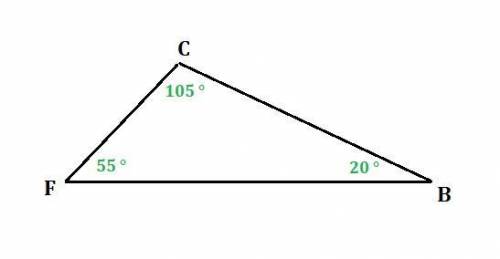
В треугольнике FBC известно, что FB >ВС > FC. Найди градусные меры ∠F, ∠B и ∠С, если один из углов равен 55 °, а другой — 105 °.
∠С=105°, ∠F=55°, ∠B=20°
Объяснение:
Известно, что сумма углов треугольника равна 180°, поэтому третий угол треугольника будет равен: 180°-55°-105°=20°.
Против большей стороны в треугольнике лежит больший угол (против меньшей стороны — меньший угол).
Из рисунка видим, что напротив стороны FB лежит ∠С, напротив ВС лежит ∠F, напротив FC лежит ∠В.
Расположим стороны треугольника по убыванию, а под ними расположим углы, которые лежат напротив этих сторон:
FB > ВС > FC
∠С > ∠F > ∠В
105° > 55° > 20°
Следовательно:
∠С=105°, ∠F=55°, ∠B=20°
Больший угол равен 180°-60°=120° (так как сумма углов при любой стороне параллелограмма равна 180°). Этот угол делится диагональю на углы 30° и 90°.
Тогда в прямоугольном треугольнике образованном диагональю и двумя сторонами против угла 30° лежит катет, равный половине гипотенузы, то есть В = 2А. Тогда 3А=45
А=15см, а В = 30см.