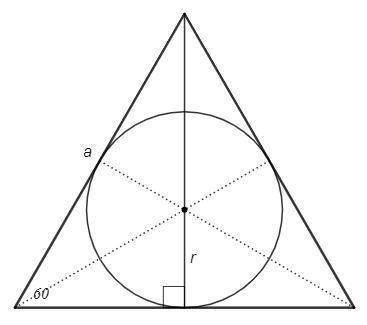
Центр вписанной окружности треугольника - точка пересечения биссектрис.
В равностороннем треугольнике все биссектрисы являются также высотами и медианами.
h =a*sin60 =√3/2 a
Медианы треугольника делятся точкой пересечения в отношении 2:1 от вершины.
r =1/3 h =√3/6 a
a =6/√3 r =6/√3 *4√3 =24
Или
Точка пересечения биссектрис - центр вписанной окружности (O).
В равностороннем треугольнике все биссектрисы являются также высотами и медианами.
OH=4√3 (радиус), AC=2AH
В треугольнике (AOH) с углами 30, 90 стороны относятся как 1 :√3 :2
(катет против угла 30 равен половине гипотенузы, далее по теореме Пифагора)
AH=OH*√3 => AC=OH*2√3 =4√3 *2√3 =24

1. Е=120°, М=120°, К=60°, F=60°
2. P=60°, М=60°, N=120°, L=120°
(Надеюсь правильно)
Объяснение:
1.
Рассмотрим треугольники EFK и FMK,они равны по 3 признаку равенства треугольников.
Треугольник EFK равнобедренный,углы при основании равнобедренного треугольника равны=> угол k= углу f=30°. E= 180-(30*2)= 120°
В параллелограмме противоположные углы равны=> E=M=120°, K=F=60°
2.
Рассмотрим треугольники NPL и NML они равны по 3 признаку равенства треугольников. В равносторонеем треугольнике углы равны=> угол N= углу L= углу P= 180/3=60°
В параллелограмме противоположные углы равны=> угол P= углу М=60°, угол N= углу L=120°