1) Так как по заданию дана правильная четырехугольная пирамида с равными рёбрами, то боковые грани такой пирамиды - это равносторонние треугольники.
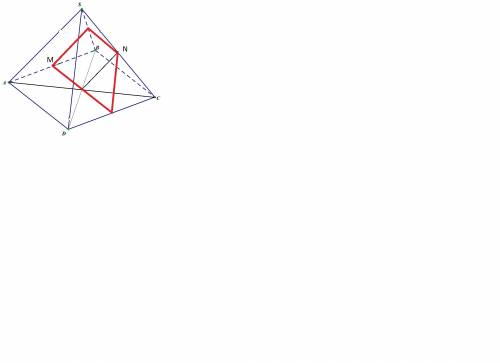
Из точки N проводим прямую, параллельную SA, до пересечения с плоскостью основания. В треугольнике ASC это средняя линия, точка пересечения прямой из точки N - это центр основания, точка О.
Через точки М и О проводим след сечения заданной плоскости с основанием. Этот след пересекает ребро СД в его середине - в точке К.
Так как отрезок МК параллелен ВС (это линия пересечения боковой грани BSC и основания, то в грани BSC из точки N проводим прямую, параллельную ВС. Отрезок NP - это след сечения заданной плоскостью грани BSC.
Осталось соединить точки М и Р и сечение готово.
Оно представляет собой равнобокую трапецию. Основание её равно стороне основания пирамиды, а остальные стороны трапеции как средние линии треугольников боковых граней равны половине стороны основания.
2) Угол между прямыми SA и MN найдём методом параллельного переноса.
Перенесём отрезок MN точкой М в точку А, то есть на половину стороны основания. Тогда точка N при сдвиге на половину стороны основания переместится в середину бокового ребра CSD (на длину средней линии этой грани). Получим медиану треугольника АSD.
Так как боковая грань - равносторонний треугольник с углами по 60 градусов, то угол между ребром SA и медианой этой грани равен 30 градусов.
Если построить окружность по трем точкам К, М и С, то точка А неизбежно попадет на неё. В самом деле, предположив, что это не так, и рассматривая углы КАС и КА1С (А1 - точка пересечения АС с окружностью, проходящей через К, М, С), можно увидеть, что в треугольнике АА1К внешний угол равен внутреннему, поскольку
угол КА1С = 180 - угол КМС и угол КАС = 180 - угол КМС (это задано в условии).
Поэтому точка А может лежать только на построенной окружности. То есть вокруг АКМС можно описать окружность.
Если провести в четырехугольнике АКМС диагнонали АМ и КС, то
Угол ВКМ = угол КАМ + угол КМА = угол КСМ + КСА = угол ВСА (углы КАМ и КСМ - вписанные, опираются на дугу АК описанной окружности вокруг АКМС, то есть они равны, аналогично углы КМА и КСА вписанные, опираются на дугу КА, поэтому и они равны).
Теперь видно, что в треугольниках АВС и ВКМ угол В общий, а угол ВКМ = угол ВСА, то есть эти треугольники подобны.
При этому ВК (в тр-ке ВКМ) соответствует ВС (в тр-ке АВС), а ВМ соответствует АВ.
а) следует непосредственно из подобия треугольников АВС и ВКМ.
б) из условия следует, что площадь тр-ка ВКМ составляет 1/9 от площади тр-ка АВС. Поэтому соответственные стороны этих подобных треугольников отсносятся как 1/3. То есть АВ/ВМ = 3