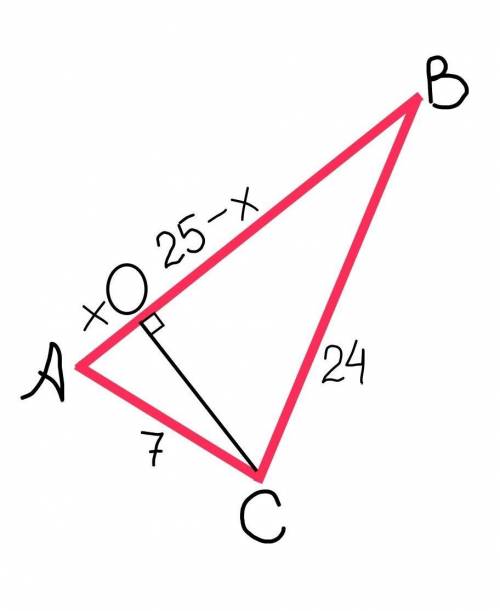
Дано:
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.
У нас есть 2 прямоугольных треугольника — ΔABD & ΔACD.
Они имеют общую гипотенузу AD, как дано и нарисовано в картинке.
<D — делится на пополам, так как через неё проходит биссектриса AD, тоесть — <BDA == <CDA.
Третий признак равенства прямоугольных треугольников таков: если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
И так как <BDA == <CDA; AD — общий, то ΔABD == ΔACD.
И так как треугольники равны, то каждый из катетов попарно равен другому, тоесть: AB == AC.
Отсюда Х= 2,8см/14 = 0,2см.
Стороны равны 0,6см и 0,8см
Проверяем: периметр равен 2*(0,6+0,8) = 2,8