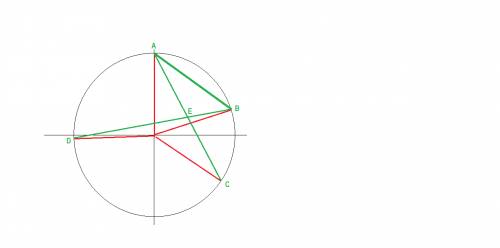
сделаем построение по условию
соединим точки А и В
найдем углы треугольника АЕВ
<ABD -вписаный - опирается на дугу (AD)
его величина РАВНА половине размера дуги
<ABD=<ABE=92/2=46
<ВАС -вписаный - опирается на дугу (ВС)
его величина РАВНА половине размера дуги
<ВАС=<BAE=48/2=24
два угла нашли
сумма углов в треугольнике 180 град
<AEB =180 -<ABE -<BAE =180-46-24=110 град
угол <AEC =180 - развернутый
<BEC и <AEB -смежные
<BEC =180-<AEB =180-110=70 град
ОТВЕТ <АЕВ=110 ; <ВЕС=70
Треугольник АВС, АВ=ВС=10, АС = 16, точка М - точка пересечения биссектрис треугольника - центр вписанной окружности, точка К - цент пересечения серединных перпендикуляров - центр описанной окружности, ВН - высота треугольника на АС, МН - радиус вписанной окружности, ВК - радиус описанной окружности и лежит за пределами треугольника, угол В - тупой,
АН=НС=16/2=8, ВН = корень (АВ в квадрате - АН в квадрате) = корень(100-64)=6
Полупериметр = (10+10+16)/2=18
Площадь треугольника = 1/2АС х ВН = 8 х 6=48
радиус вписанной = площадь/полупериметр = 48/18=2,67 = МН
радиус описанной = произведение сторон / 4 х площадь = 10 х 10 х 16 / 4 х 48= 8,33=ВК
расстояние между центрами = ВК - ВН+МН=8,33-6+2,67=5
Дорисовываем диагональ, и получится прямоугольный треугольник.
У квадрата все стороны равны, значит в прямоугольном треугольнике можем вычислить нужную нам сторону за т Пифагора
диалональ²= 1сторона²+ 2сторона²
диагональ ²= (4√2)²+(4√2)²
диагональ²=16+2+16+2
диагональ²=36
диагональ=6