1) cos 71° = 0,3256.
2) cos 18° 25' = 0,9488.
3) Радиус описанной окружности 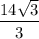 см.
см.
Объяснение:
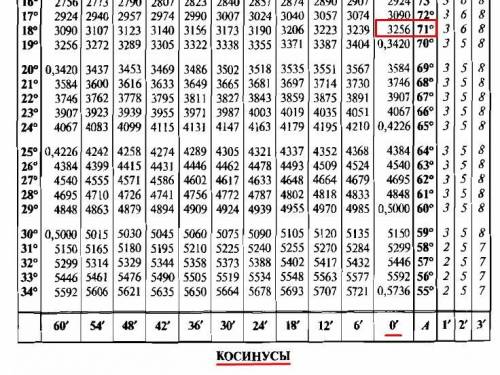
1) Найти cos 71°.
Воспользуемся таблицами Брадиса В.М. для синусов и косинусов углов.
Для нахождения косинусов углов таблицу используем снизу вверх, значения углов берем из правой колонки, значения минут из нижней строки.
Находим значение cos 71° 0' (см. приложение 1).
cos 71° = 0,3256.
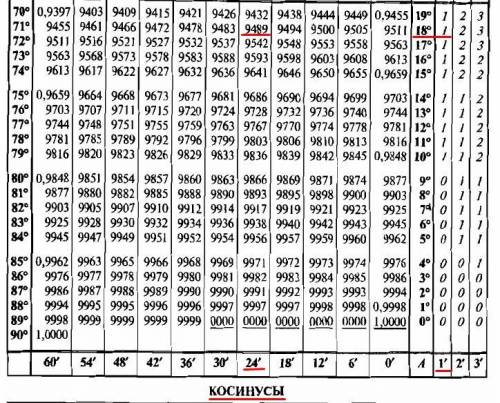
2) Найти cos 18° 25'.
Находим по таблице косинусов в правой колонке угол 18°.
В нижней строке нет значения 25', поэтому берем ближайшее значение минут: 24', и сделаем поправку на 1 минуту. Поправка равна 1 (см. приложение 2).
cos 18° 24' = 0,9489.
Так как с увеличением острого угла значение косинуса уменьшается, то поправку нужно отнять.
9489 - 1 = 9488.
Тогда cos 18° 25' = 0,9488.
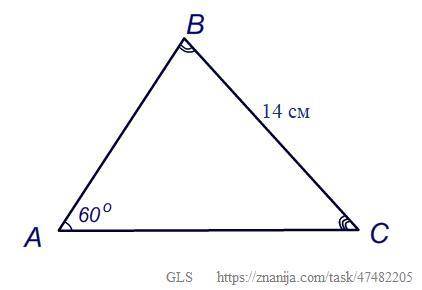
3) Найти радиус описанной около треугольника окружности, если известен угол треугольника ∠A = 60° и длина противолежащей стороны BC = 14 см.
Рисунок прилагается (приложение 3).
Радиус описанной окружности найдем по формуле: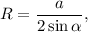
где R - радиус описанной окружности, a - сторона треугольника, α - противолежащий этой стороне угол.
По таблице:
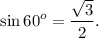
Подставим данные задачи:
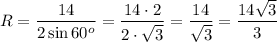 (см).
(см).
Радиус описанной окружности 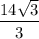 см.
см.
ответ: V=64√5см³
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³