

Как известно, сумму углов многоугольника находят по формуле:
180° · (n - 2), где n - число сторон многоугольника.
Сумма углов правильного пятиугольника равна:
180° · (5 - 2) = 180° · 3 = 540°.
Т.к. у правильного пятиугольника все углы равны, то один его внутренний угол равен 540° : 5 = 108°.
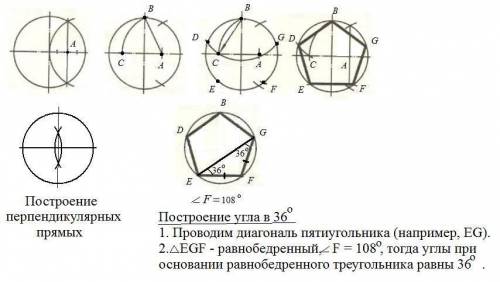
Построение правильного пятиугольника (см. рисунок)
1. Строим окружность произвольного радиуса.
2. Строим два перпендикулярных диаметра этой окружности (одна из простейших задач на построение с циркуля и линейки).
3. Делим один из радиусов пополам. Получаем точку А.
4. Измеряем расстояние АВ и строим точку С.
5. Строим окружность этого же радиуса АВ с центром в точке В.
6. Получаем точки D и G.
7. Из точек D и G строим окружности этого же радиуса и получаем точки Е и F.
8. Соединяем точки В, D, Е, F, G - получаем правильный пятиугольник.
Построение перпендикулярных прямых (деление отрезка пополам)
1. Строим один из диаметров.
2. Строим окружности большего (или меньшего) радиуса с центрами в концах построенного диаметра.
3. Соединяем точки пересечения построенных окружностей.
4. Полученная прямая и есть прямая, перпендикулярная данной (и делящая данный отрезок пополам) – в нашем случае, перпендикулярная диаметру.
Построение угла в 36° - см. рисунок
Задача решена.
Відповідь:
Пояснення:
1. Правильние 1, как к касательним, и 2 , как радиуси, утверждения
2. Правильние 3) , как радиуси, и 4) из свойств расположения центра описаной окружности
3. 8+7=15
Из равенства касательних, проведенних из одной точки
4. /_BAD=2×/_BOD=120° как соотношение центрального и вписаного укла круга
5. Р□=2(12+16)=56 из свойств трапеции, в которую можно вписать круг ( как и в задаче 3)
6. Из свойств четирехугольников, которие можно вписать в круг
/_А+62°=180°
/_А=180-62=118°