ответ:Номер 1
ЕК||АD при секущей FB,т к
<МFB=<АВF=56 градусов,как внутренние накрест лежащие
<С+<М=180 градусов,как односторонние при EK||AD и секущей СМ,тогда
<М=180-72=108 градусов
Номер 2
Углы при основании равнобедренного треугольника равны между собой
<1=56 градусов
<2=<3=(180-56):2=62 градуса
Номер 3
<АВЕ=<DBC=15 градусов,как вертикальные
Треугольник DBC
<D=48 градусов
<B=15 градусов
<С=180-(48+15)=180-63=117 градусов
Треугольник АСF
<F=64 градуса
<DCB+<ACF=180 градусов,как смежные
<АСF=180-117=63 градуса
<А=180-(64+63)=180-127=53 градуса
Объяснение:
На сторонах АВ и ВС треугольника ABC отметили точки К и М так, что АК:КВ=3:4 , АМ:МС=7:2. Разложить векторы BC, KC, BM, KM по базису (m;n), где AK=m, MA=n.
Объяснение:
На сторону АВ приходится 3+4=7 частей, сторону АС- 9 частей.
1) Вектор ВС=( по правилу разности )= АС- АВ=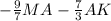 =
=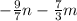 .
.
2) Вектор КС=( по правилу разности )= АС- АК=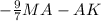 =
=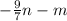 .
.
3) Вектор ВМ=( по правилу разности )= АМ- АВ=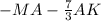 =
= .
.
3) Вектор КМ=( по правилу разности )= АМ- АК=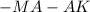 =
=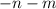 .
.