Поскольку АС=ВС, то треугольник АВС-равнобедренный(значит углы при основании равны).
Сумма углов=180 градусов.
180-52=128.
128/2=64 градуса(углы А и В)
Следуя из теоремы о смежных углах:<CBD=180-64=116 градусов.
ответ: <CBD=116 градусов.
Рассмотрим треугольники АОD и ВОС, которые образовались в следствие пересечения плоскости отрезком. Они будут подобны, так как их углы равны. Представил АО как Х, тогда ВО будет равно 15-х. Согласно теореме подобия мы делаем выводы:
= 
=> 
=
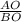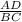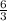
х = 30-2х, отсюда х = 10, следовательно => АО=10, а ВО=5 (15-10).
После этого нам надо найти ОD и ОС по теореме Пифагора, так как треугольники AOD и BOC - прямоугольные:
ОD = √АО²-АD² = √100-36 = 8 сантиметров
ОС = √ВО²-ВС² = √25-9 = 4 сантиметров
Найдем теперь проекцию этого отрезка на плоскость:
CD = OC+ОD = 4+8 = 12 сантиметров
ОТВЕТ: 12 сантиметров
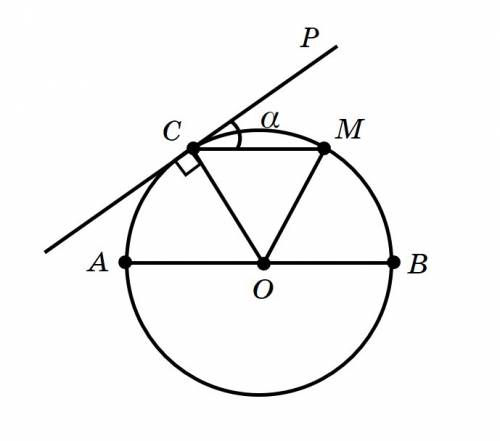
Пользуясь рисунком, (см. вложение) и зная, что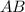 
— диаметр окружности, 
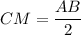— хорда окружности, определим 
.
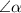В окружности половиной диаметра являются радиусы, значит, эти радиусы будут равны и хорде: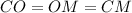 
В образовавшемся треугольнике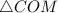 
получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по 
.
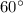Как известно, точка касания касательной к окружности и радиуса окружности пересекаются под прямым углом (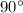
).
Отсюда следует, чтобы узнать 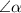, нужно найти разность развёрнутого угла (
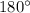) от суммы других известных углов:
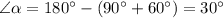
ответ: 30°
Т.к. АС=ВС, то треугольник АВС-равнобедренный, следовательно,
<A=<B=(180-52)/2=128/2=64
По теореме о смежных углах, <CBD=180-<B=180-64=116
ответ: 116