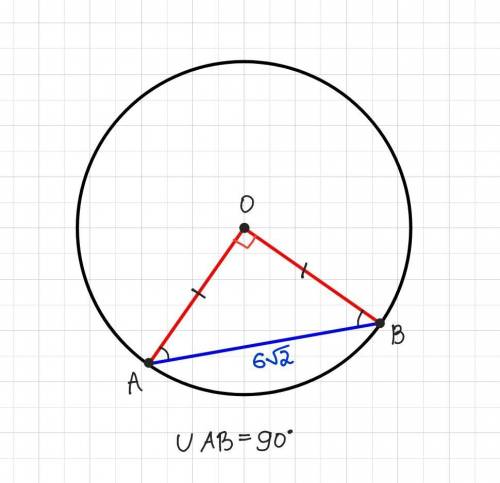
Дано: коло (О; R), AB - хорда, АВ= 6√2 см, ◡АВ= 90°
Знайти: С (довжину кола)
Розв'язання.
Проведемо радіуси ОА і ОВ до кінців хорди АВ. OA=OB=R.
∠АОВ — центральний, це означає що його градусна міра дорівнює градусній мірі дуги, на яку він спирається.
∠АОВ= ◡АВ= 90°.
Як бачимо, ΔАОВ - прямокутний рівнобедрений (оск. ∠АОВ= 90°, ОА=ОВ=R).
Хорда АВ дорівнює 6√2 см, тоді за т.Піфагора у ΔАОВ:
АВ²= ОА²+ОВ²;
(6√2)²= 2ОА²;
72= 2ОА²;
ОА²= 36;
ОА= 6 (–6 не може бути).
Отже, R= 6см.
Тепер знаходимо довжину кола.
За формулою С= 2πR.
С= 2•π•6;
С= 12π, або С= 12•3,14= 37,68 (см)
Відповідь: 12π см або 37,68 см.
См. рисунок.
Так как AK биссектриса, то ∠BAK=∠KAD=45° ⇒ ΔABK равнобедренный (так как ∠ABK=90°, а ∠AKB=180°-90°-45°=45°), а значит BK=AB=4 cм.
BC=BK+KC=4+5=9 cм.
Площадь прямоугольника равна
S=AB*BC=4*9=36 см².