Сделаем рисунок к задаче.
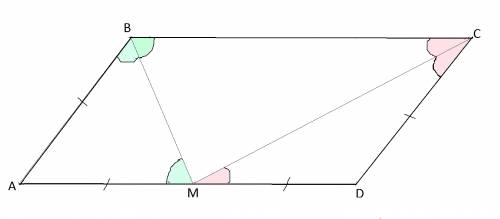
Обозначим вершины параллеограмма привычными буквами АВСD.
Проведем биссектрисы углов В и С, которые пересекутся на АD в точке М.
Биссектрисы образовали со сторонами параллелограмма треугольники, причем
∠ СВМ= ∠ АМВ по свойству углов при пересечении параллельных прямых и секущей, а
∠ АВМ= ∠МВС - как половины угла В.
То же самое с углами ВСМ и СМD.
Раз углы при основании ВМ Δ АВМ и основании СМ Δ СМD равны,
оба этих треугольника - равнобедренные.
В треугольнике АВМ сторона АВ равна стороне АМ,
В треугольнике МDС сторона МD равна стороне СD.
Но АВСD- параллелограмм, и стороны АВ и CD равны по определению.
Следовательно, АМ=MD и АD=2АВ ( или 2 CD, что одно и то же)
Р АВСD= 2( АВ+АD) Подставим в значение периметра 2 АВ вместо AD.
Р АВСD= 2( АВ+2АВ)
30= 6 АВ
АВ=5 см
Ответ: Длина короткой стороны параллелограмма равна 5 см
равносторонний конус, => осевое сечение конуса правильный треугольник со стороной 40 см
конус: диаметр основания d =40 см, R=20 см
высота конуса Н = высоте правильного треугольника, вычисленного по формуле:
h= \frac{a \sqrt{3} }{2}h=
2
a
3
а - сторона правильного треугольника
h=H= \frac{40* \sqrt{3} }{2} =20* \sqrt{3}h=H=
2
40∗
3
=20∗
3
V= \frac{1}{3}* \pi R^{2} *HV=
3
1
∗πR
2
∗H
V= \frac{1}{3}* \pi *20^{2} *20 \sqrt{3} = \frac{8000 \sqrt{3} \pi }{3}V=
3
1
∗π∗20
2
∗20
3
=
3
8000
3
π
ответ: V конуса=(8000√3*π)/3 см³
Відповідь:
Пояснення:
Ich habe eine Katze namens Lola. Sie ist klein, also trinkt sie Milch. Ich liebe sie!