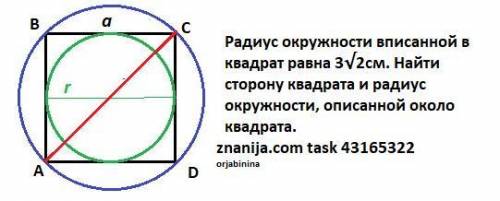
Радиус окружности вписанной в квадрат равна 3√2см. Найти сторону квадрата и радиус окружности, описанной около квадрата.
Объяснение:
1) Тк окружность вписана , то она касается всех сторон квадрата и диаметр окружности равен стороне квадрата : а₄=2r=2*3√2=6√2 (cм).
2) Если теперь около квадрата ABCD описать окружность, то диагональ квадрата AC равна диаметру окружности .
ΔАВС-прямоугольного , по т. Пифагора АС=√( (6√2)²+(6√2)²)=12 (см).
Поэтому радиус , описанной около квадрата , окружности R=12:2=6 (см).
Объяснение:
83.
Дано: ∠MDE;
DP ⊥ LF; PL = PF.
Доказать: ∠LDP = ∠FDP.
Доказательство:
Рассмотрим ΔDLP и ΔDPF - прямоугольные (DP ⊥ LF).
PL = PF (условие)
DP - общая.
⇒ ΔDLP = ΔDPF (по двум катетам)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠LDP = ∠FDP.
84.
Дано: ΔDEF;
EK ⊥ DF; DK = FK;
Доказать: ED = EF.
Доказательство:
Рассмотрим ΔKDE и ΔKEF - прямоугольные (EK ⊥ DF) .
DK = FK (условие)
КЕ - общая.
⇒ ΔKDE = ΔKEF (по двум катетам)
В равных треугольниках против равных углов лежат равные стороны.⇒ ED = EF.
85.
Дано: прямая а;
∠DAB = ∠EAB; ∠DBA = ABE;
Доказать: ΔBAD = ΔBAE.
Доказательство:
Рассмотрим ΔBAD и ΔBAE.
∠DAB = ∠EAB; ∠DBA = ABE (по условию)
АВ - общая.
⇒ ΔBAD и ΔBAE (по стороне и двум прилежащим углам. 2 признак)