Точки Т и Р лежат на стороне ВС, значит четырехугольник АТРД трапеция, углы при основании равны, значит равнобедренная. Радиус вписанной в него окружности равен корень из 3, следовательно высота трапеции равна 2 корня из 3. Обозначим высоту из точки Т ТК. В треугольнике АТК угол А 60 градусов. синус 60 градусов равен отношению ТК к АТ. АТ = 2 корня из 3 делим на синус 60 градусов. Получаем АТ=6, АК = 3, как катет , лежащий против угла в 30 градусов. Трапеция равнобедренная, то высота, проведенная из точки Р, отсекает такой же отрезок от точки Д. Далее, раз в трапецию можно вписать окружность, то сумма боковых сторон равна сумме оснований. Получаем 3+3+2ТР= 12 ТР=3, АД= 9
1) АО=ОВ=R=CD/2=40/2=20
2)OD=20 ⇒ ОМ = 20-4 = 16
3) Р/м ΔАОМ: ∠М=90°, по т.Пифагора: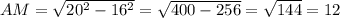
4) АВ=АМ+МВ=12+12=24
ответ: 24