(См. рисунок) Прямые ND и DC пересекаются в точке D: ND ∩ DC = D
⇒ по теореме стереометрии о пересекающихся прямых через них проходит плоскость и притом только одна – плоскость γ ("гамма").
Две точки прямой NC лежат в плоскости "гамма", значит вся прямая NC лежит в этой плоскости: NC ⊂ γ. Так как прямая KN пересекает NC в точке N, принадлежащей прямой NC: N ∈ NC, то KN и NC также лежат в одной плоскости. Итак, точки N, D, C, K образуют плоскость γ.
Поскольку плоскость α параллельна плоскости β: α║β,
то по теореме о пересечении двух параллельных плоскостей третьей: линии пересечения будет параллельны друг другу ⇒ KN ║ DC ⇒ углы
NDC и KND – односторонние; их сумма равна развёрнутому углу:
∠NDC + ∠KND = 180° ⇒ ∠KND = 180° - ∠NDC = 180° - 80° = 100°.
ответ: ∠KND = 100°
Доказательство в объяснении.
Объяснение:
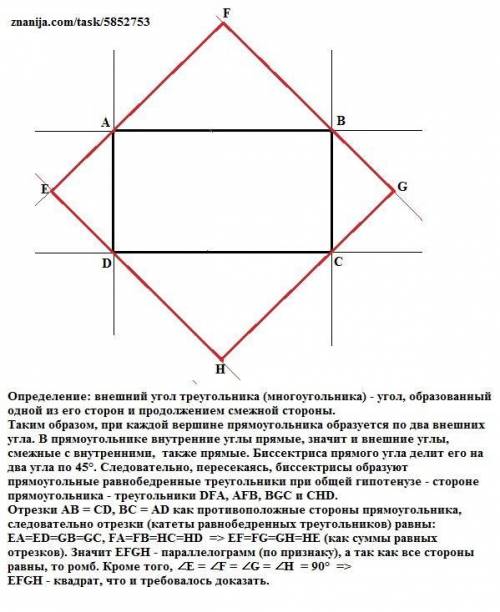
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.
1) Найдем длины векторов. I→аI=√(3²+4²+0²)=√25=5;
I→bI=√(4²+4²+2²)=√36=6;
скалярное произведение →а*→b= I→аI*I→bI*cos∝;
→а*→b=5*6**cos150°=30*(-√3/2)=-15√3
2)I→аI=√(1²+0²+3²)=√10;
I→bI=√(5²+5²+0²)=√50=5√2;
скалярное произведение →а*→b= I→аI*I→bI*cos∝;
→а*→b=√10*5√2**cos30°=5√20*(√3/2)=5*2√5*√3/2=5√15