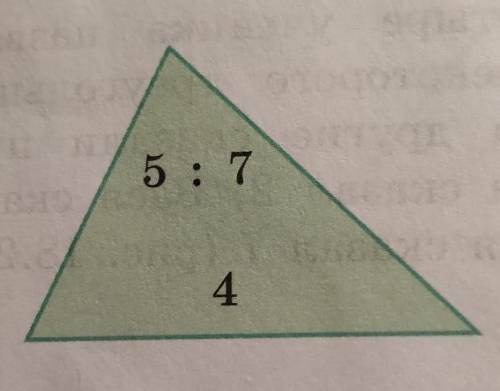
1.) Радиус цилиндра 2 см, а диагональ осевого сечения 5 см. Найдите:
a) Высоту цилиндра
Прямоугольный треугольник. Т. Пифагора
Н² = 5² - 4² = 9, ⇒ Н = 3
б) Площадь осевого сечения
Осевое сечение - прямоугольник
S = 3*4 = 12
в) Диаметр основания
Диаметр основания = 2 радиуса = 4
2.) Образующая конуса равна 6 м и наклонена к плоскости основания под углом 60 градусов. Найдите площадь основания конуса, площадь осевого сечения.
Прямоугольный треугольник. Гипотенуза = 6, катет = радиусу лежит против угла 30, значит, R = 3
высота конуса = √(36 - 9) = √27 = 3√3
площадь основания конуса = S кр = πR² = π*9= 9π
Осевое сечение = треугольник, котором боковые стороны = 6, основание = 6 и высота = 3√3
S = 1/2*6*6*3√3 = 54√3
3.) Найдите площадь большого круга и длину экватора шара, если его радиус 2 м.
S= πR² = π*4 = 4π(м²)
C = 2πR = 2π*2 = 4π(
8. <DBC=63°
9. P = 36 ед.
10. Не полное условие.
Объяснение:
Дуга BD равна 2*27° = 54° (так как вписанный угол, опирающийся на эту дугу, равен половине градусной меры этой дуги).
Дуга BDAC = 180°, так как ВС - диаметр.
Дуга DAC = DDAC - BD = 180-54 = 126°. =>
<DBC = 63° (вписанный, равен половине градусной меры дуги, на которую он опирается).
9. Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники. В нашем случае эти биссектрисы имеют общую точку Е на стороне ВС. Значит
АВ = ВЕ и EC = CD => BC = 2AB.
AB = СD и BC = AD (противоположные стороны параллелограмма).
Рabcd = 6*AB = 36 ед.