рассмотрим прямоугольный треугольник ABC в которм угол А - прямой, угол В = 30 градусам а угол С = 60.
Приложим к треугольнику АВС равный ему треугольник АВD. Получим треугольник BCD в котором B = D = 60 градусов, следовательно DC = BC. Но по построению АС 1/2 ВС, ч т д
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам.
рассмотрим прямоугольный треугольник АВC, у которого катет АС равен половине гипотенузы АС.
Приложим к треугольнику АВС равный ему треугольник ABD. Получит равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу, поэтому каждый из них = 60 градусам. Но угол DBC = 2 угла ABC, следовательно угол АВС = 30 градусов,ч т д
1) Если внешний угол при вершине В равен 111градусов, то внутренний как смежный угол равен 180-111=69 град. Т.к. треугольник равнобедренный, то углы В и А равны. Следовательно, если сумма всех углов треугольника равна 180градусов, угол при вершине С = 180 - (69+69) = 42 градуса.
2) аналогично. (180-20):2= 80, т.е. по 80 градусов угол В и угол А.
3) пусть х - коэффициент пропорциональности. тогда 2х+3х+7х=180. х=15 градусов. Меньший угол тогда 2 умножить на 15 = 30градусов
4) аналогично. х+2х+4х+8х=360. х=24 грудса, т.е. меньший угол.
5) сумма углов параллелограмма = 360градусов. т.к. диагональ разделяет угол при вершине параллелограмма на 2 части, то этот угол будет равен 61+47 = 108градусов.Другой угол параллелограмма будет равен = (360 - (2·108))÷2 = 73 градуса
6) пусть меньшее основание х, тогда большее равно х+16. По свойству средней линии трапеции: 2·18 = х + (х+16), отсюда х = 10. ответ: 10.
В треугольнике ABC высоты проведенные из вершин A и B относятся как 7: 9. Найди отношение сторон BC и AC
Объяснение:
Пусть АК⊥ВС , ВН⊥АС . Тогда АК:ВН=7:9
В ΔАКС , sinC=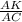
. В ΔНВС , sinC=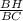 
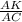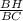Приравняем правые части
= 
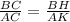или 
или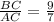 
.