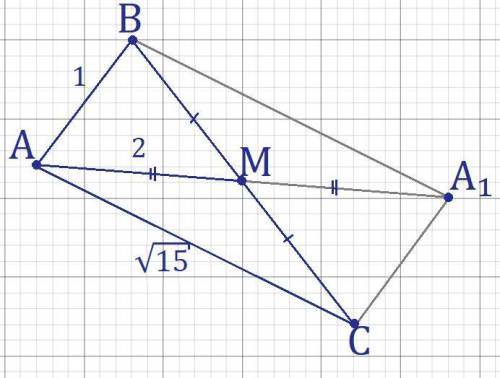
Дано: AB=1; AC=√15; BM=MC; AM=2.
Найти: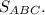 
A₁ ∈ AM; AM=A₁M
ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.
ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:
AA₁² = (2AM)² = (2·2)² = 4² = 16;
AC²+CA₁² = (√15)²+1² = 15+1 = 16;
16 = 16 ⇒ AA₁² = AC²+CA₁².
Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.
ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.
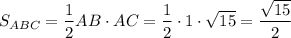как площадь прямоугольного треугольника (∠BAC=90°).
ответ: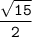 
ответ:S=16π
Объяснение:в основании образуется треугольник, состоящий из двух радиусов, к-ые относятся к дуге с 60°, и сторонной, полученной сечением квадрата. Сторону квадрата находим по Пифагору: √(a²+a²) = 4√2, a = 4. Основание треугольника так же равно 4. Этот треугольник, в первую очередь, является равнобедренным, так как имеет две равных сторон (радиусов окружности), но по той причине, что вершина равна 60, это правильный треугольник. Следовательно, все его стороны равны, что указывает, что радиусы равны 4. Зная радиус, мы можем найти длину окружности: 2πr=4π. Высотой цилиндра является сторона квадрата, т.к. второй пересекает его параллельно оси. Отсюда S=4π*4=16π
<B = 30°.
Теорема о 30-градусном угле прямоугольного треугольника такова: Катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Против угла B — лежит катет AC, что и означает, что AC — равен половине гипотенузы AB.
AC = 12 = AB/2 => AB = 12*2 = 24.
Формула вычисления радиуса описанной окружности около прямоугольного треугольника такова:
То есть, в прямоугольном треугольнике — радиус описанной окружности равен катету, противолежащему углу 30-градусов.
Вывод: R = 12.