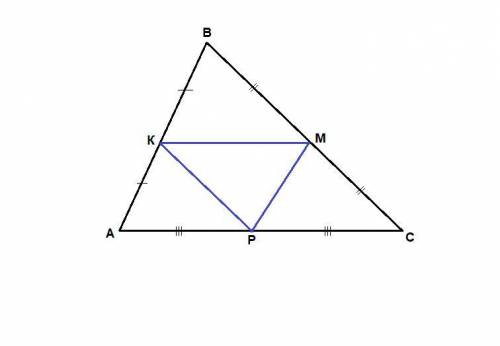
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
МР = АВ/2, ⇒
МР = АК = КВ
КР = ВС/2, ⇒
КР = ВМ = МС
КМ = АС/2, ⇒
КМ = АР = РС.
Таким образом ΔАКР = ΔКВМ = ΔРМС = ΔМРК по трем сторонам.
Для ΔАКР и ΔАВС:
∠А - общий,
∠АКР = ∠АВС как соответственные при пересечении параллельных прямых КР и ВС секущей АВ, значит
ΔАКР подобен ΔАВС по двум углам.
Значит треугольнику АВС будут подобны и все остальные треугольники, равные треугольнику АКР:
ΔКВМ подобен ΔАВС
ΔРМС подобен ΔАВС
ΔМРК подобен ΔАВС
АВ=АС(по усл.), ВД=ДС ( по усл.), АД - общая сторона => треуг. подобны (по 3 признаку равенства треугольников) .
Д.П. : построим ВС.
Рассмотрим треуг ВАС:
угол А=60, ВАС-р/б => АН-(высота) является биссектрисой => угол ДАС=60градусов/2=30 градусов.