Как расположены окружность с радиусом r и прямая ( d – расстояние от центра окружности до прямой), если: А) d = 2 см, r = 40 мм; В) d = 3 см, r = 5 см; С) d = 30 мм, r = 3 см.

👇

Открыть все ответы

Ответ:

Rkkshv

12.11.2022

ответ: Б.) 52/4=13 см сторона ромба10:2=5 см половина диагонали ромба13*13=169 квадрат стороны 5*5=25 квадрат половины диагонали169-25=144 квадрат половины другой диагоналиКорень из 144 равен 12 см - половина второй диагонали12*2=24 см вторая диагональ

А.) А) треугольник АОВ прямоугольный, и АО = одна вторая АС, ВО = одна вторая ВD. Значит АО = 3дм а ВО = 4дм. По теореме Пифагора АВ = корень квадратный из 3 во второй степени + 4 во второй степени = корень квадратный из 9 + 16 = корень квадратный из 2

4,5(65 оценок)

Ответ:

Demongirl1

12.11.2022

Задача 2.

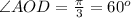
$\angle{AOD} = \frac{\pi}{3} = 60^{o}$

Задача 3.

Проекциями прямых параллельных сторонам исходного параллелограмма будут прямые, проходящие через т. пересечения диагоналей и середины сторон у параллелограмма проекции

Объяснение:

Дано

АВСД - прямоугольник

АВ = 6 см

АД = 2√3 см

Найти

уг. м/ду АС и ВД

Решение

Очевидно, что АС и ВД - диагонали прямоугольника.

Обозначим т. пересечения как т. О

Тогда уг.АОД - искомый угол между диагоналями.

Обозначим

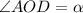
${\angle AOD} = \alpha$

По св-вам прямоугольника, его диагонали равны и в т. пересечения делятся пополам. Т.е.

АО = ОС = ВО = ОД

По Т. Пифагора можно найти диагонали:

ВД² = АВ² + АД²

BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2}

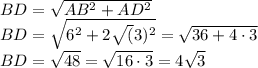
$BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2} = \sqrt{36 + 4 \cdot3} \\ BD = \sqrt{48} = \sqrt{16\cdot3} = 4 \sqrt{3}$

Соответственно

АС = ВД = 4√3

Рассмотрим тогда треугольник АОД, он равнобедренный, т.к.

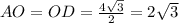
$AO = OD = \frac{4\sqrt3}{2} = 2 \sqrt{3}$

Так же 2√3 равна и сторона АД нашего прямоугольника.

То есть - мы получаем, что

АО = ОД = АД = 2√3

Следовательно - ∆АОД равносторонний,

а это означает, что искомый угол AOД

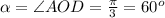
$\alpha = \angle{AOD} = \frac{\pi}{3} = 60^{o}$

Для особо дотошных:

По Т. косинусов имеем:

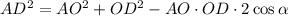
$\small {AD^2=AO^2+OD^2-AO\cdot OD \cdot 2\cos{ \alpha}}$

Отсюда

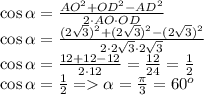
${\cos{ \alpha} = \frac {AO^2+OD^2-AD^2}{2 \cdot AO\cdot OD }} \\ {\cos{ \alpha} = \frac {(2 \sqrt{3})^2 +(2 \sqrt{3})^2 -(2 \sqrt{3})^2 }{2 \cdot 2 \sqrt{3} \cdot 2 \sqrt{3} }} \\ { \cos \alpha = \frac {12 + 12 - 12}{2 \cdot12}} = \frac{12}{24} = \frac{1}{2} \\ \cos \alpha = \frac{1}{2} = \alpha = \frac{\pi}{3} = 60^{o}$