А₁А₂ = 2 см
Объяснение:
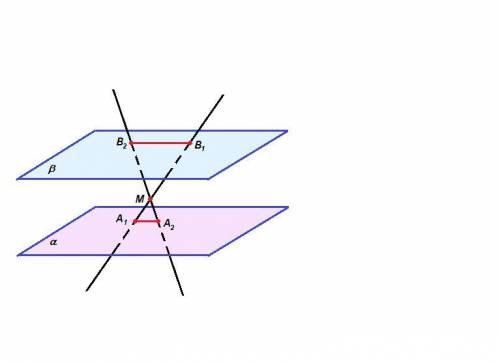
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
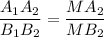
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
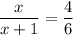
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
Рассм. тр. ACD
угол ACD = 90
угол CAD = 30 (накрест лежащие BC || AD сек. AC)
⇒ угол ADC = 60
Катет лежащий против угла в 30 равен половине гипотенузы ⇒ СВ=1/2AD
Расс. тр. ABC
угол BAC = углу CAD = 30 (по условию AC биссектриса)
угол BCA = 30 (по условию)
⇒ AB=BC
Трап. ABCD равнобедренная так как угол BAD = CDA = 60 ⇒AB=CD
Следовательно AB=BC=CD=1/2AD
P=AB+BC+CD+AD
2=1/2AD+1/2AD+1/2AD+AD
AD=0.8
AB=BC=CD=0.4
Средняя линия равна 1/2*(BC+AD) ⇒ 1/2*(0.4+0.8) = 1/2*1.2 = 0.6
средняя линия трапеции равна 0.6