Признаки равнобедренной трапеции:
1. Если углы при основании трапеции равны, то она равнобедренная.
2. Если диагонали трапеции равны, то она равнобедренная.
3. Если сумма противолежащих углов трапеции равна 180°, то эта трапеция равнобедренная.
4. Если вокруг трапеции можно описать окружность, то она равнобедренная.
Доказательство 1 признака:
Дано: ABCD - трапеция,
∠BAD = ∠CDA
Доказать: АВ = CD.
Доказательство:
Проведем высоты ВН и СК.
В треугольниках АВН и DCK:
∠ВНА = ∠СКD = 90°,
ВН = СК как расстояния между параллельными прямыми,
∠ВАН = ∠CDK по условию, ⇒
ΔАВН = ΔDCK по катету и противолежащему острому углу, значит
АВ = CD.
В правильном многоугольнике все стороны и углы равны.
Внутренний угол правильного n-угольника вычисляется по формуле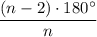
ΔABC = ΔBCD по двум сторонам и углу между ними (AB=BC=CD, ∠ABC=∠BCD), поэтому AC=BD, как соответственные стороны (AC напротив ∠ABC; BD напротив ∠BCD и эти углы равны).
ΔABD = ΔDCA по трём сторонам (AB=DC, AC=DB и AD - общая), поэтому ∠BAD=∠CDA, как соответственные углы (∠BAD напротив BD; ∠CDA напротив AC и эти стороны равны).
Сумма углов в выпуклом четырёхугольнике равна 360°.
В четырёхугольнике ABCD:
∠ABC+∠BCD+∠CDB+∠DAB = 360°
2·(∠BCD+∠CDA) = 360°
∠CDA = 360°:2-∠BCD = 180°-144° = 36°
ответ: 36°.