Доброго времени суток!
В условии ошибка : "Острый угол равен 30 см". Углы не измеряются в сантиметрах. Скорее всего, Вы имели ввиду 30°.
▔ ▔ ▔
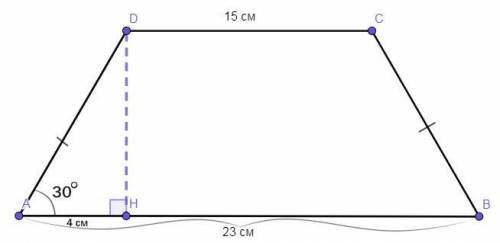
У равнобедренной трапеции острый угол равен 30°. Вычислите площадь этой трапеции, если длины оснований равны 15 см и 23 см.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
Дано:Четырёхугольник ABCD — равнобедренная трапеция (AD = CB, CD║AB).
∠DAB = 30°.
CD = 15 см.
АВ = 23 см.
Найти:S(ABCD) = ?
Решение:Из вершины ∠ADC на основание АВ опустим высоту DH.
По свойству отрезков, образованных основанием высоты в равнобедренной трапеции, имеем, что —
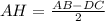
Подставим в формулу известные нам значения —
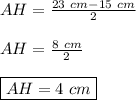
Рассмотрим ΔADH — прямоугольный.
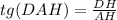
Подставим в формулу известные нам значения —
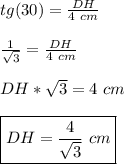
▸Площадь трапеции равна произведению полусуммы оснований и высоты◂
То есть —
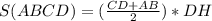
Подставим в формулу известные нам значения —
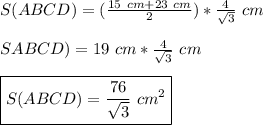

" Основой прямой призмы является равнобедренный треугольник с углом a при основании и радиусом вписанной окружности r. Диагональ боковой грани, проходящей через основание равнобедренного треугольника, наклонена к плоскости основания под углом y . Отметьте, какие из приведенных четырех утверждений правильные
1. Плоскость, проходящая через боковое ребро призмы и уентр круга, вписанного в основание, делит двугранный угол при боковом ребре призмы пополам
2. Боковое ребро призмы равна 2r*ctg*a/2*tgy
3. Одна из сторон основания призмы равна r*ctg*a/2
4. Один из двугранных углов при боковом ребре призмы равна a"
Объяснение:
1) Т.к. центр вписанной окружности лежит в точке пересечения биссектрис, то плоскостью, проходящей через боковое ребро призмы и центр круга, вписанного в основание, будет плоскость АКК₁А₁ , где АК, А₁К₁-биссектрисы нижнего и верхнего оснований.
Поэтому 1 утверждение верное.
2) Боковое ребро найдем из ΔАСС₁ -прямоугольного : СС₁=АС*tgy.
АС найдем из ΔАОН :
ΔАВС-равнобедренный. В равнобедренном
треугольнике биссектриса ВН является высотой и
медианой .АК-биссектриса, значит ∠ОАН=α/2 .
АН= r /(tgα/2 ) , 2АН=АС= =2r*ctg α/2 .
Получаем СС₁=2r*ctg α/2 *tgy.
Поэтому 2 утверждение верное.
3) 3 утверждение неверное , т.к. в п 2 найдена сторона основания АС=2r*ctg α/2 . а боковая сторона будет искаться через косинус или синус ΔАВН.
4)4 утверждение верное . Это двугранный угол , например САА₁В, т.к
АА₁⊥АС и АА₁⊥АВ и ∠ВАС=α